Intro
集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)是一种改进的EMD方法,它通过引入白噪声来解决EMD中的模态混叠问题。
模态混叠是指在分解过程中,不同时间尺度的信号成分错误地混合在一起,导致分解结果不准确。
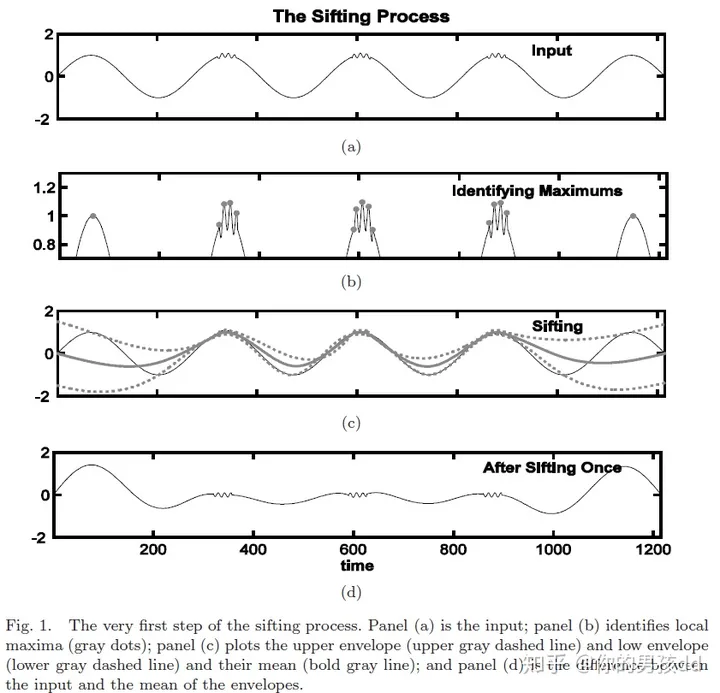
上述figure就是一个很好的例子,连续低频正弦信号上叠加了间歇性高频震动的调制信号,因为间歇性高频震动的调制信号干扰了Maximum点的选择,使得局部极值在很短的时间间隔发生多次跳变,进而使得我们的IMF并不准确,不同时间尺度的信号成分错误地混合在一起。
以下我们也通过我们写的EMD做了示范:
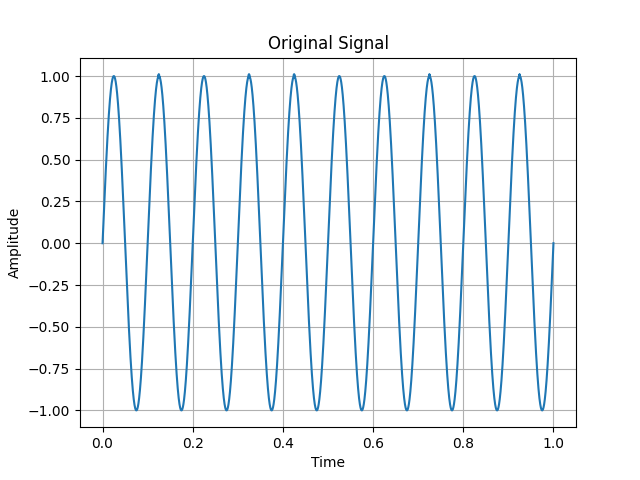
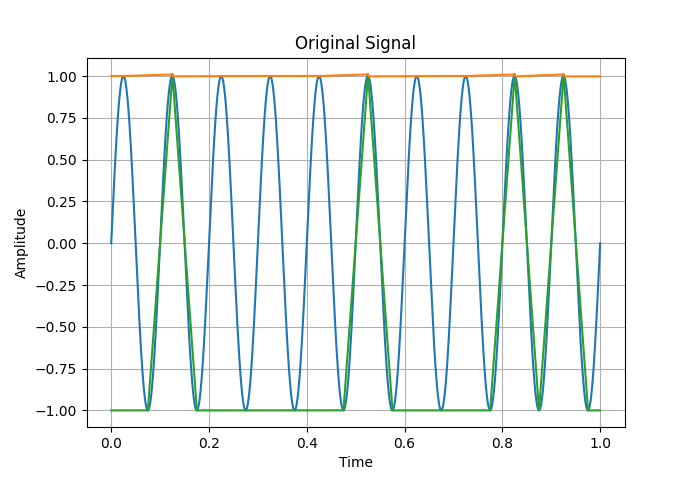
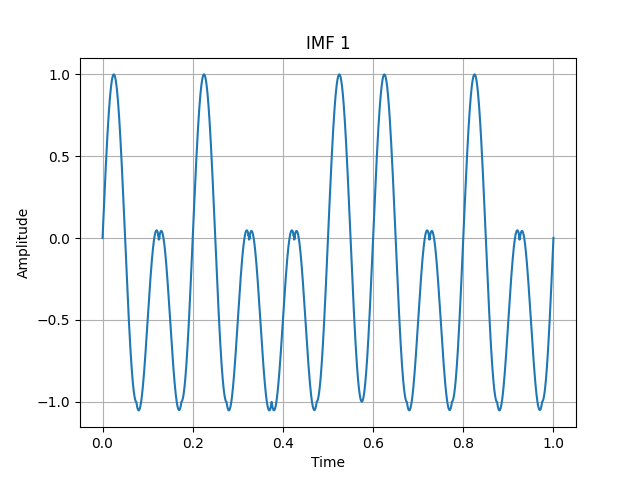
很明显,在IMF1,发生了混叠
Step by Step
为了解决这种模态混叠的现象,EEMD方法应运而生。其步骤为,
- 设定总体平均次数
- 将一个具有标准正态分布的白噪声加到原始信号上,产生一个新的信号,
- 对进行EMD
- 重复上述两步骤吗,得到IMF集合
- 对上述的IMF集合进行集合平局,得到最终的IMF,即:
Algorithm Detail
- 添加噪声对于我们的信号有什么影响
- 每次添加的信号有什么要求,加多大的噪声;(提出EEMD的Wu文章中说,标准差为0.1的噪声)
Demo Code
def EEMD(signal, max_imf = 10, tolerance = 0.01, iterations = 10):
def __extrema(signal):
max_peaks = []
min_peaks = []
for i in range(1, len(signal) - 1):
if signal[i] > signal[i-1] and signal[i] > signal[i+1]:
max_peaks.append(i)
if signal[i] < signal[i-1] and signal[i] < signal[i+1]:
min_peaks.append(i)
return max_peaks, min_peaks
def __mean_env(signal):
max_peaks, min_peaks = __extrema(signal)
max_env = np.interp(range(len(signal)), max_peaks, [signal[i] for i in max_peaks])
min_env = np.interp(range(len(signal)), min_peaks, [signal[i] for i in min_peaks])
return (max_env + min_env) / 2
def __IMF(signal):
resdiual = signal
while True:
imf = signal - __mean_env(resdiual)
resdiual = signal - imf
if np.mean(imf) < tolerance:
break
return imf, resdiual
mean = np.mean(signal)
std = np.std(signal)
signal = (signal - mean) / std
imfss = []
signals = []
min_imf = max_imf
tmp_imf = max_imf
for index in range(iterations):
imfs = []
noise = np.random.randn(len(signal))
noise = noise * 0.1
new_signal = signal + noise
signals.append(new_signal)
tmp_imf = max_imf
while True:
imf, residual = __IMF(new_signal)
imfs.append(imf)
max_peaks, min_peaks = __extrema(residual)
if len(max_peaks) < 2 or len(min_peaks) < 2:
tmp_min = len(imfs)
if tmp_min < min_imf:
min_imf = tmp_min
break
if np.abs(np.std(residual)) < tolerance or tmp_imf == 0:
tmp_min = len(imfs)
if tmp_min < min_imf:
min_imf = tmp_min
break
new_signal = residual
tmp_imf -= 1
imfss.append(imfs)
imf_ans = []
for i in range(min_imf):
imf = 0
for j in range(iterations):
imf += imfss[j][i]
imf = imf / iterations
imf_ans.append(imf)
signal_ans = 0
for signal in signals:
signal_ans += signal
signal_ans = signal_ans / iterations
residual_ans = signal_ans
for imf in imf_ans:
residual_ans = residual_ans - imf
imf_ans = [imf * std + mean for imf in imf_ans]
residual_ans = residual_ans * std + mean
signal_ans = signal_ans * std + mean
return imf_ans, residual_ans, signal_ansResults
通过EEMD,结果如下:
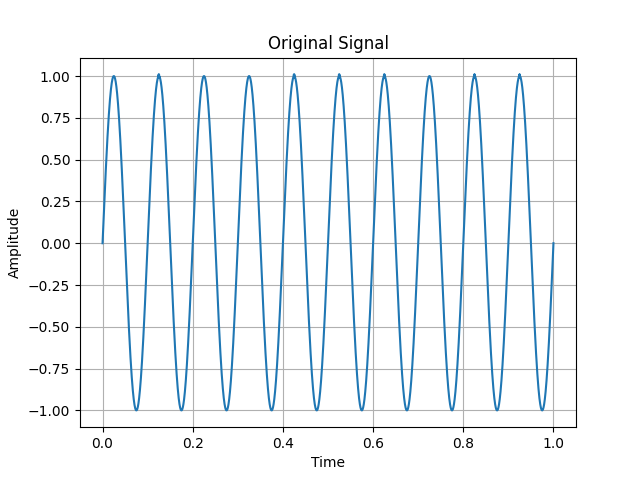
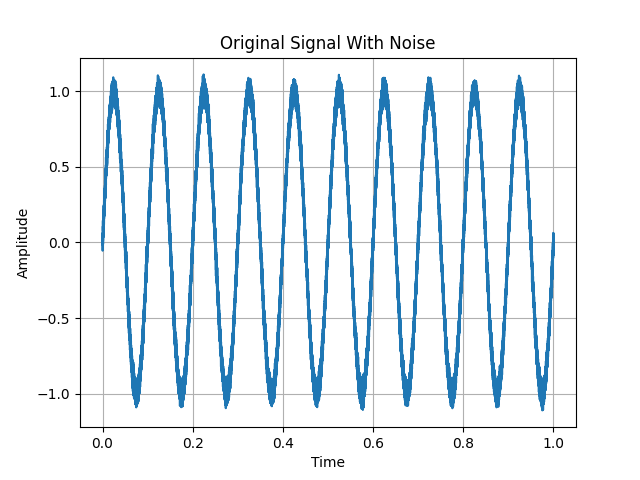
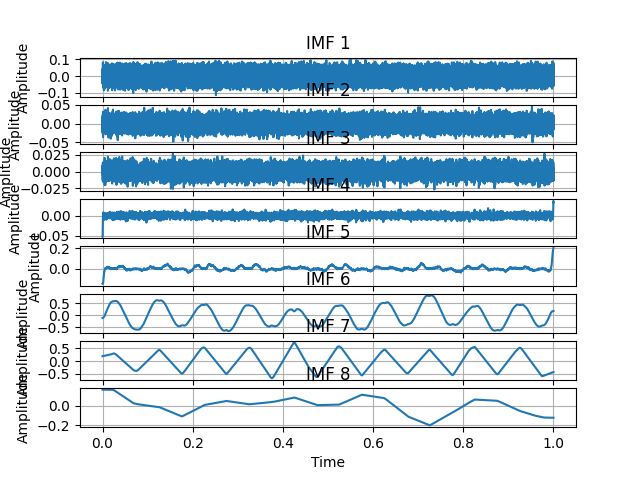
EEMD的前几个IMF将高频噪声和白噪声过滤,在IMF7显示了信号原有的模态