在大多数现实世界的预测问题中,我们的预测所带来的不确定性具有重要价值。相较于仅仅提供点估计,了解预测范围能够显著改善许多商业应用的决策过程。Quantile loss就是为例帮助我们了解预测范围的loss function。
Quantile loss用于衡量预测分布和目标分布之间的差异,特别适用于处理不确定性较高的预测问题。
What is quantile
What is a prediction interval
预测区间是对预测的不确定性进行量化的一种方法。它为结果变量的估计提供了概率上限和下限的范围。
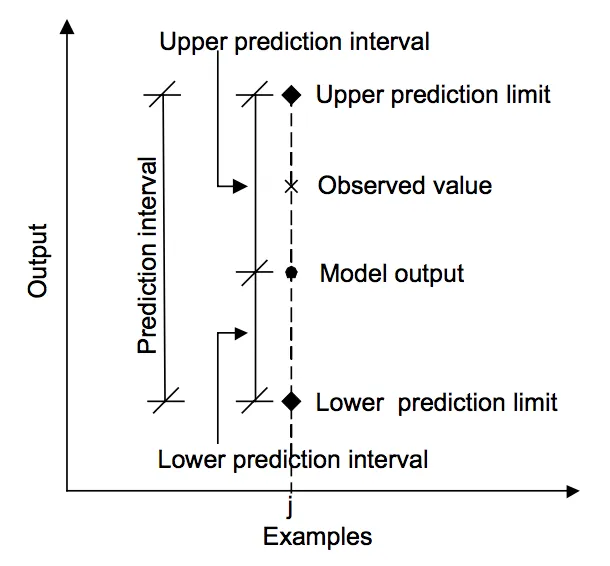
输出本身是随机变量,因此具有分布特性。预测区间的目的在于了解结果的正确性可能性。
What is Quantile Loss
在Quantile loss中,我们将预测结果和目标值都表示为分位数形式,例如,我们可以用预测的α分位数来表示预测结果,用真实值的α分位数来表示目标值。然后,Quantile loss衡量了这两个分布之间的差异,通常使用分位数损失函数来计算。
分位数回归损失函数(Quantile Regression Loss)用于预测分位数(Quantile)。例如,对于分位数为0.9的预测,应该在90%的情况下做出过高的预测。
对于一条数据,prediction是,真实值是,mean regression loss for a quantile q:
一系列prediction数据来通过minimize这个loss function后,得到quantile -
Intuitive Understanding
在上述的回归损失方程中,由于 q 的取值范围在 0 到 1 之间,当进行过高预测( > )时,第一项将为正并占主导地位;而当进行过低预测( < )时,第二项将占主导地位。当 q 等于 0.5 时,过低预测和过高预测将受到相同的惩罚因子,从而得到中位数。q 的值越大,相比于过低预测,过高预测将受到更严厉的惩罚。例如,当 q 等于 0.75 时,过高预测将受到 0.75 的惩罚因子,而过低预测将受到 0.25 的惩罚因子。模型做出过高预测的可能性的难度将会是过低预测可能性的3倍,从而得到 0.75 分位数。
Why Quantile loss
Quote
“同方差性”,“恒定方差假设”
在最小二乘回归中,预测区间基于一个假设,即残差在自变量的各个取值上具有恒定的方差。这假设被称为“同方差性”或“恒定方差假设”。
这个假设是基于对回归模型中误差项的性质的一种合理假设。在最小二乘回归中,我们假设因变量的观测值是由真实值和一个误差项组成的,而这个误差项是独立同分布的,即在每个自变量取值上都具有相同的分布。
如果残差在自变量的各个取值上具有恒定的方差,意味着误差的大小不会随着自变量的变化而发生显著的变化。这样的话,我们可以使用统计方法来计算出预测区间,这个区间能够给出对未来观测值的置信度。
然而,如果恒定方差假设不成立,也就是残差在自变量的取值上具有不同的方差,那么最小二乘回归的结果可能会出现问题。在这种情况下,预测区间可能会低估或高估预测的不确定性,导致对未来观测值的置信度估计不准确。
Quantile Loss Regression可以提供合理的预测区间,即使对于具有非恒定方差或非正态分布的残差也是如此