树状数组(Fenwick Tree),也被称为二叉索引树(Binary Indexed Tree,BIT),其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。它可以以的时间得到任意前缀和,并同时支持在时间内支持动态单点值的修改,空间复杂度为
我们希望BIT可以完成的操作是:
- 更改存储在索引I处的值。(这称为点更新操作)
- 查找长度为k的前缀之和。(这称为前缀和查询)
Origin
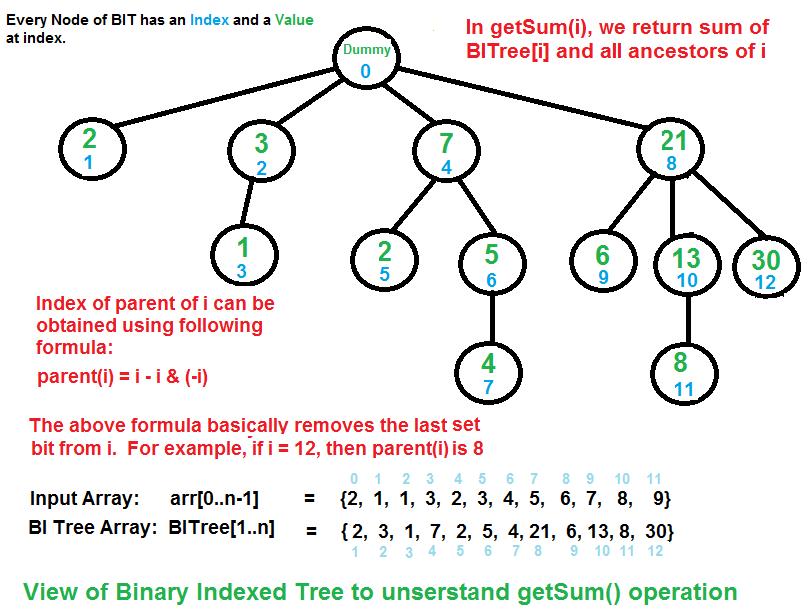
按照Peter M.Fenwick的说法,正如所有的整数都可以表示成2的幂和,我们也可以把一串序列表示成一系列子序列的的和。采用这个想法,我们可将一个前缀和划分成多个子序列的和,而划分的方法与数的2的幂和具有极其相似的方式。一方面,子序列的个数是其二进制表示中1的个数,另一方面,子序列代表的f[i]的个数也是2的幂。
Step by Step
lowbit(x:int) -> int
该函数返回参数转为二进制后,最后一个1的位置所代表的数值,例如:
lowbit(34) -> 2
lowbit(12) -> 4
lowbit(8) -> 8
在coding时,可以使用位运算(~i + 1) & i来计算最后一位1的值,它的原理在于使得最小位数上的1在~i + 1和i上都为1,而其它位置上则不会同时为1,因此使用and运算可以得到最后一位1的值
同时,具有trick的点在于,实际coding的时候,lowbit函数写为:
def lowbit(x):
return x & (-x)并不需要做+1操作,这是因为这是因为当我们对整数 i 取负数 -i 时,其二进制表示中只有最右边的 1 保持不变,而其余位都会取反。然后我们再将 i 与 -i 进行按位与操作 &,结果会保留 i 中最右边的 1,而将其他位都变为 0。这个技巧的原理基于补码表示法,在补码表示法中,正整数的补码和其本身相同,负整数的补码是将其绝对值的二进制表示取反后加 1。所以很多语言在coding的时候,-i所做操作就是~i+1
lowbit()
Build Array BIT (Binary Indexed Tree)
二叉索引树一般由数组实现
在Fenwick Tree结构中,需要一个数组BIT来维护数组的前缀和,有:
code实现: