平稳描述的是信号的统计特性不随时间变化的特性。平稳性是许多信号处理算法和理论分析的基础假设,特别是在随机过程和时间序列分析中。
一个平稳信号需要满足两个主要条件:
- 均值的平稳性:信号的统计平均值(均值)不随时间变化。换句话说,无论我们何时观察信号,其平均值都保持不变。对于连续时间信号,这意味着信号的平均值对于所有时间点都是恒定的;对于离散时间信号,这意味着信号的平均值对于所有时间步长都是恒定的。
均值与n无关,即于哪次观察信号无关
2. 自相关函数的平稳性:信号的自相关函数仅取决于时间间隔,而不是绝对的时间点。自相关函数是衡量信号在不同时间点的相似性的一种方法。对于平稳信号,如果我们将信号在时间点t和时间点t+τ的值进行比较,这种比较的结果(即自相关)只与时间间隔τ有关,而与具体的时间点t无关。
自相关函数与时间n无关,之与时移m有关
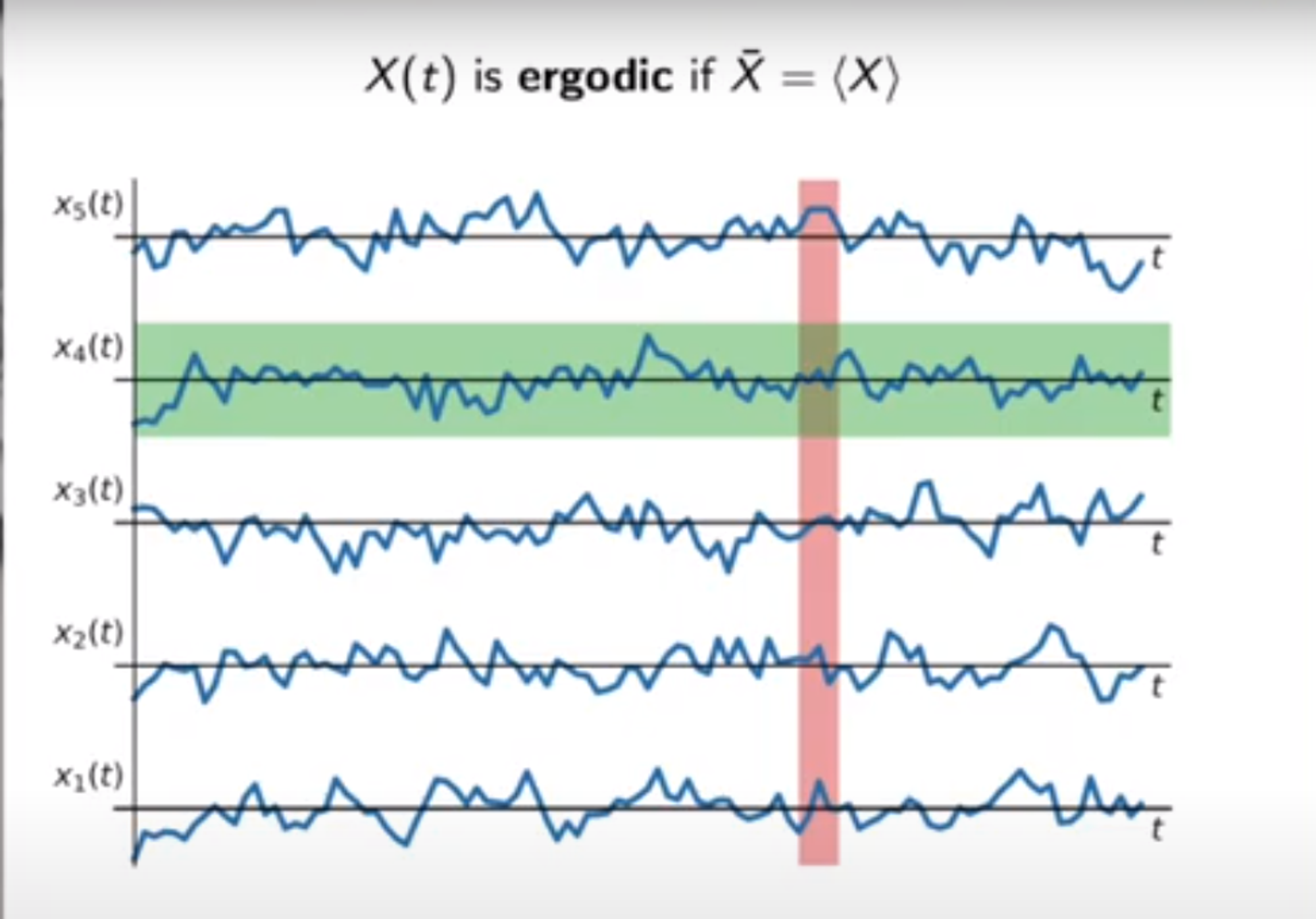
平稳信号具有Ergodicity,即各态历经,即多样本集合平均和单一样本时间平均相同
在实际应用中,完全平稳的信号是非常罕见的。大多数实际信号都是非平稳的,它们的统计特性(如均值、方差、自相关等)会随时间变化。然而,有些信号可以在一定的时间范围内近似为平稳,这种信号被称为“宽平稳”(Wide-Sense Stationary, WSS)信号。宽平稳信号的统计特性在观察的时间范围内大致保持不变,这使得它们可以用线性时不变系统进行有效分析。
平稳信号的概念对于信号处理和系统分析非常重要,因为许多信号处理技术,如傅里叶变换、功率谱密度分析、滤波器设计等,都是基于信号的平稳性假设。如果一个信号不是平稳的,那么在应用这些技术之前,我们可能需要对信号进行预处理,如去趋势、差分、归一化等,以使其满足平稳性的要求,或者使用专门为非平稳信号设计的分析方法,如非平稳时间序列分析、小波变换、经验模态分解等。