Fourier Transform

Almost Fourier Transform

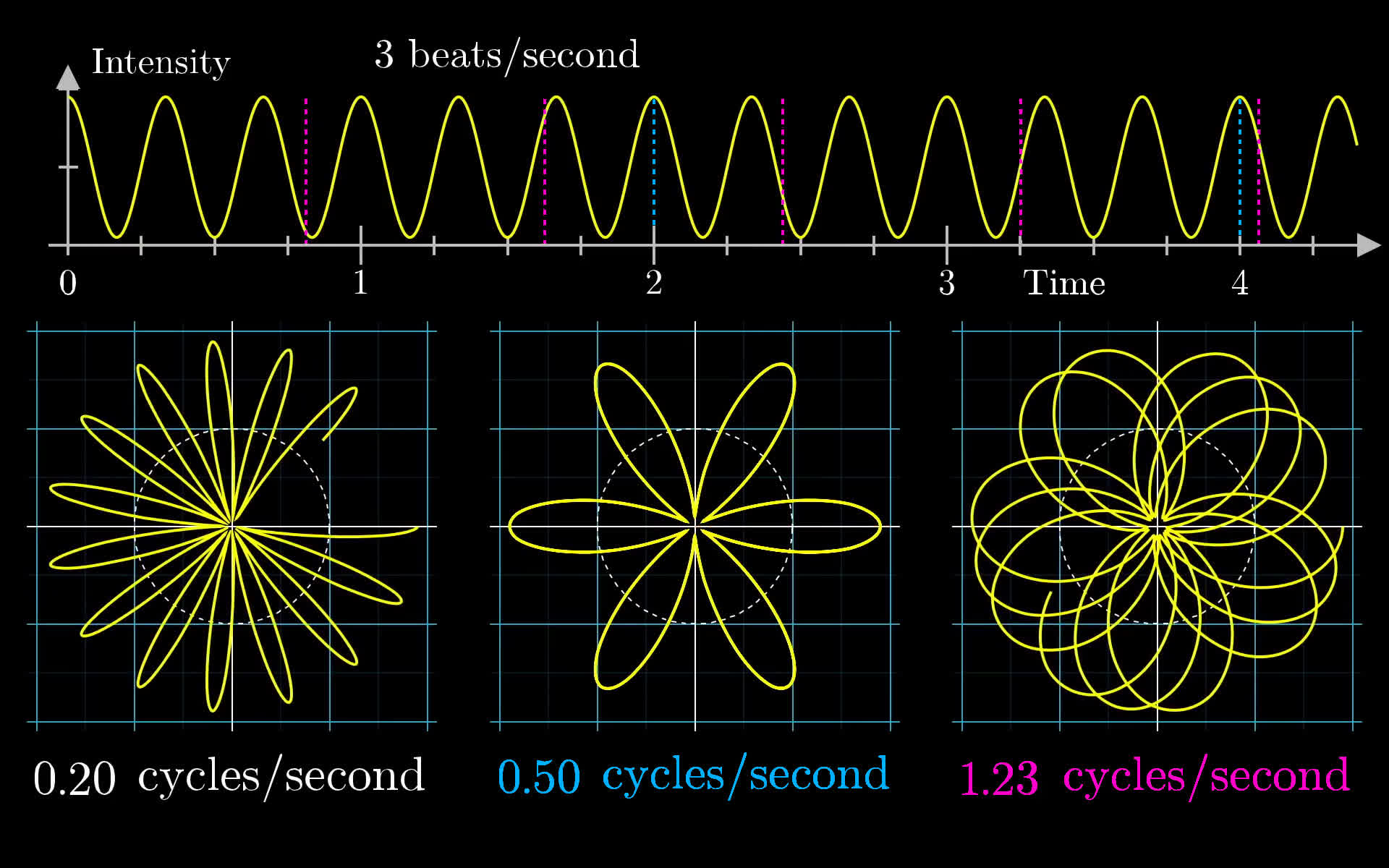
It is important to see there are 2 different frequencies here:

1. The frequency of the original signal
2. The frequency with which the little rotating vector winds around the circle

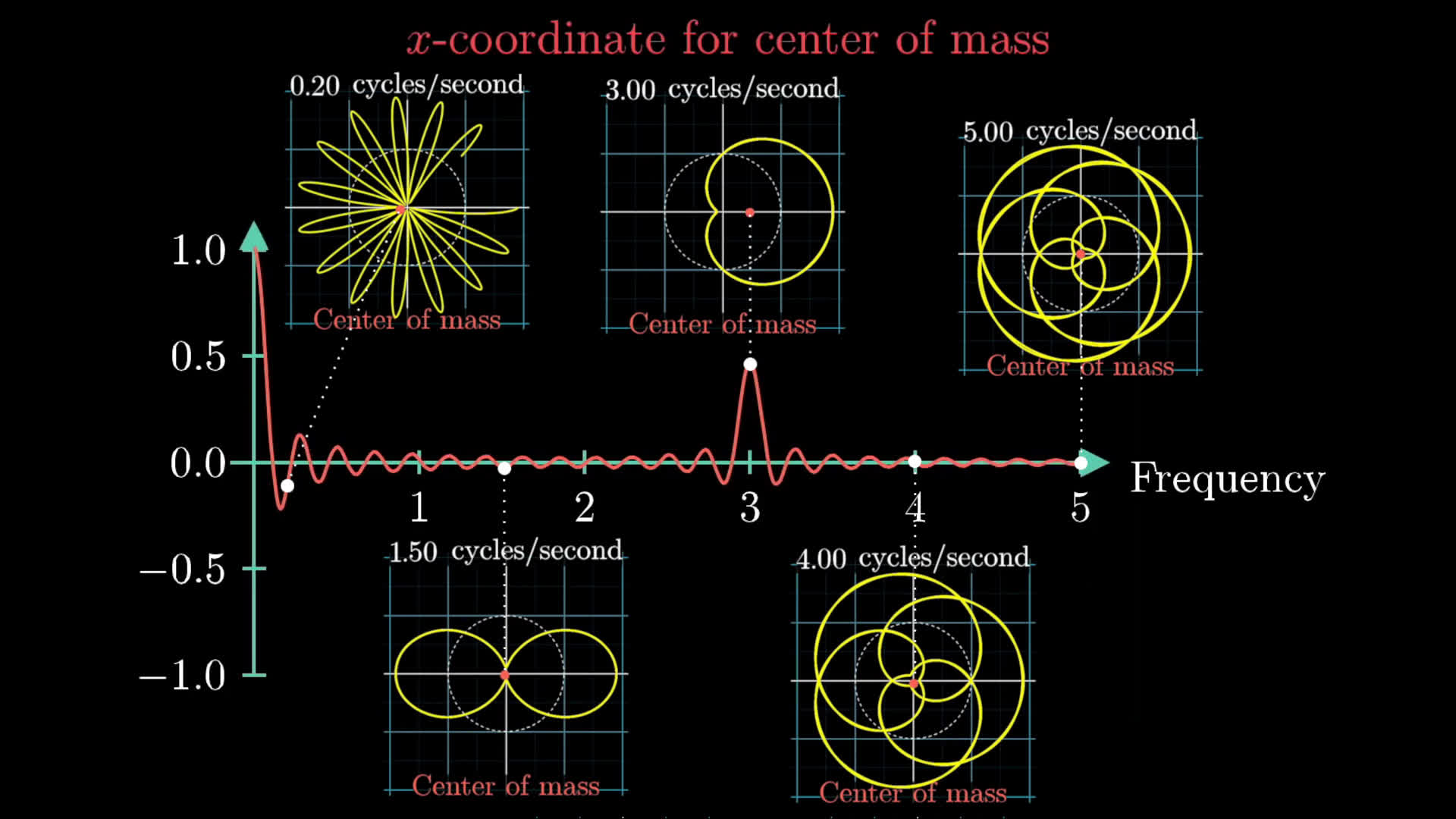
Different patterns appear as we wind up this graph, but it is clear that the x-coordinate for the center of mass is important when the winding frequency is 3; The same number as the original signal

这个发现就是Fourier transform的基础

而如何将一维信息拉到平面中，很容易想到设计complex plane，如何describe rotating at a rate of $f$, 用：

$$e^{2\pi ift}$$

因为在Fourier transform中，convention way是顺时针旋转，所以使用$e^{-2\pi ift}$，那如何衡量center of mass呢，如下图：

$$\frac{1}{N}\sum _{k=1}^{N}g(t_k)e^{-2\pi if{t}_k}$$

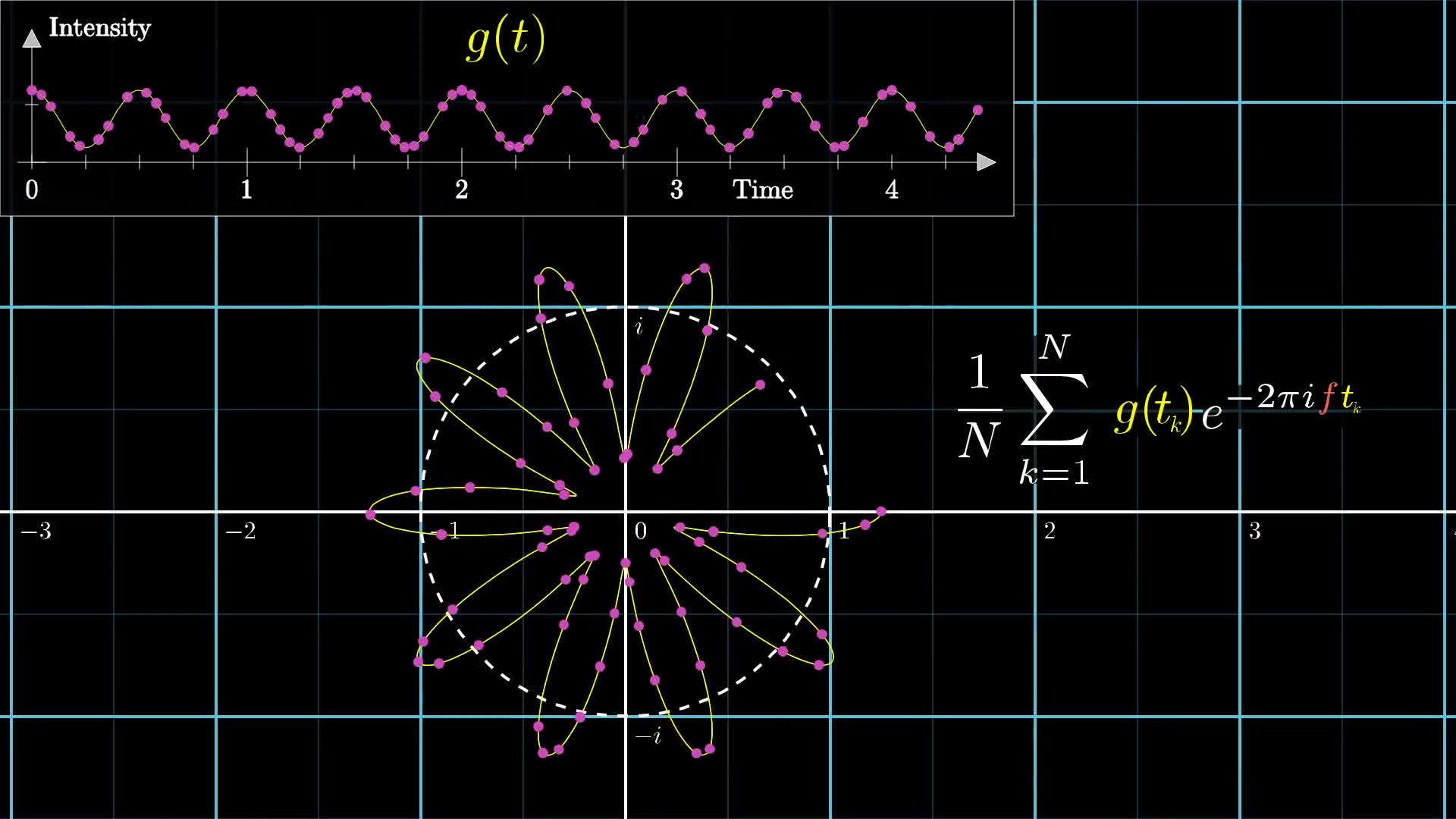
然后more points → continuous：

$$\frac{1}{t_2-t_1}{\int }_{t_1}^{t_2}g(t)e^{-2\pi ift}dt$$

这个就是Almost Fourier Transform, 但是实际情况上，Fourier transform倾向于得到scaled center mass，越长的time，旋转越多圈，其Fourier transform也会成倍放大

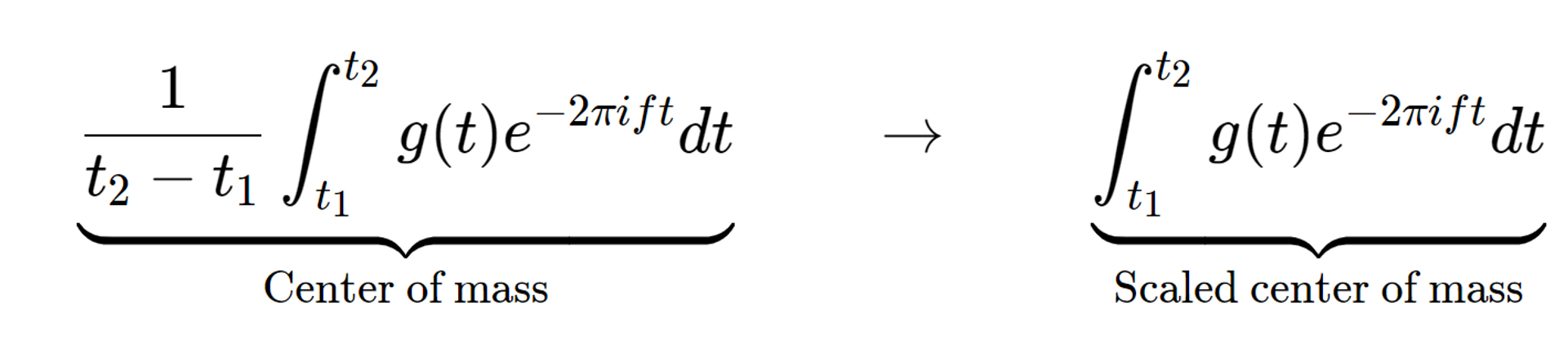
Fourier Transform (FT)

$$\hat{g}(f)={\int }_{t_1}^{t_2}g(t)e^{-2\pi ift}dt$$

一般来说，Fourier transform的bounds在$-\infty \to \infty$

$$\hat{g}(f)={\int }_{t_1}^{t_2}g(t)e^{-2\pi ift}dt$$

Inverse Fourier Transform

$$g(t)={\int }_{-\infty }^{\infty }\hat{g}(f)e^{2\pi ift}df$$

Discrete-time Fourier Transform(DTFT)

$$x[n]\underset{\text{IDTFT}}{\overset{\text{DTFT}}{\rightleftharpoons }}X(\omega )orX(e^{j\omega })$$ $$X(\omega )=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}$$

Hint

Z transform: $X(z)={\sum }_{n=-\infty }^{\infty }x(n)z^{-n}$

After DTFT, the signal $X(\omega )$ will have period $2\pi$

$$X(\omega +2\pi )=\sum _{n=-\infty }^{\infty }x[n]e^{-j(\omega +2\pi )n}=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}=X(\omega )$$

IDTFT:

$$x(n)=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }X(\omega )e^{j\omega n}d\omega$$

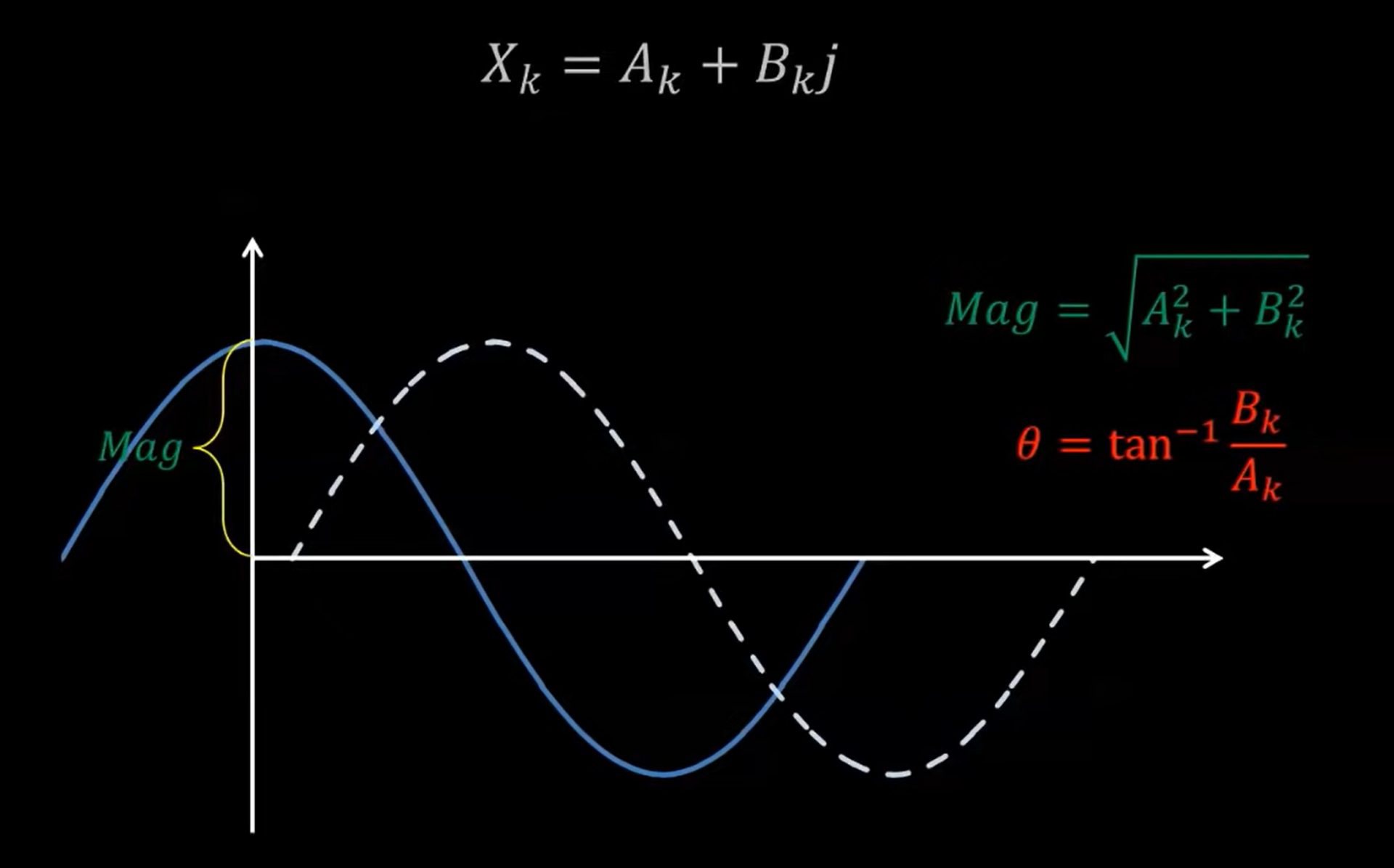
Also, for $X(\omega )$, it have polar form and rectangular form

• Polar form:

$$X(\omega )=|X(\omega )|\angle X(\omega )$$

• Rectangular form:

$$X(\omega )=X_r(\omega )+j{X}_i(\omega )$$

so, magnitude and angle

$$\begin{gathered} |X(\omega )|=\sqrt{{X_r(\omega )}^2+{X_i(\omega )}^2} \\ \angle X(\omega )={\tan }^{-1}[\frac{X_i(\omega )}{X_r(\omega )}] \end{gathered}$$

Complex Fouerier Series

为了解决热方程和弦振动，因此有了傅里叶级数；

复数形式推导

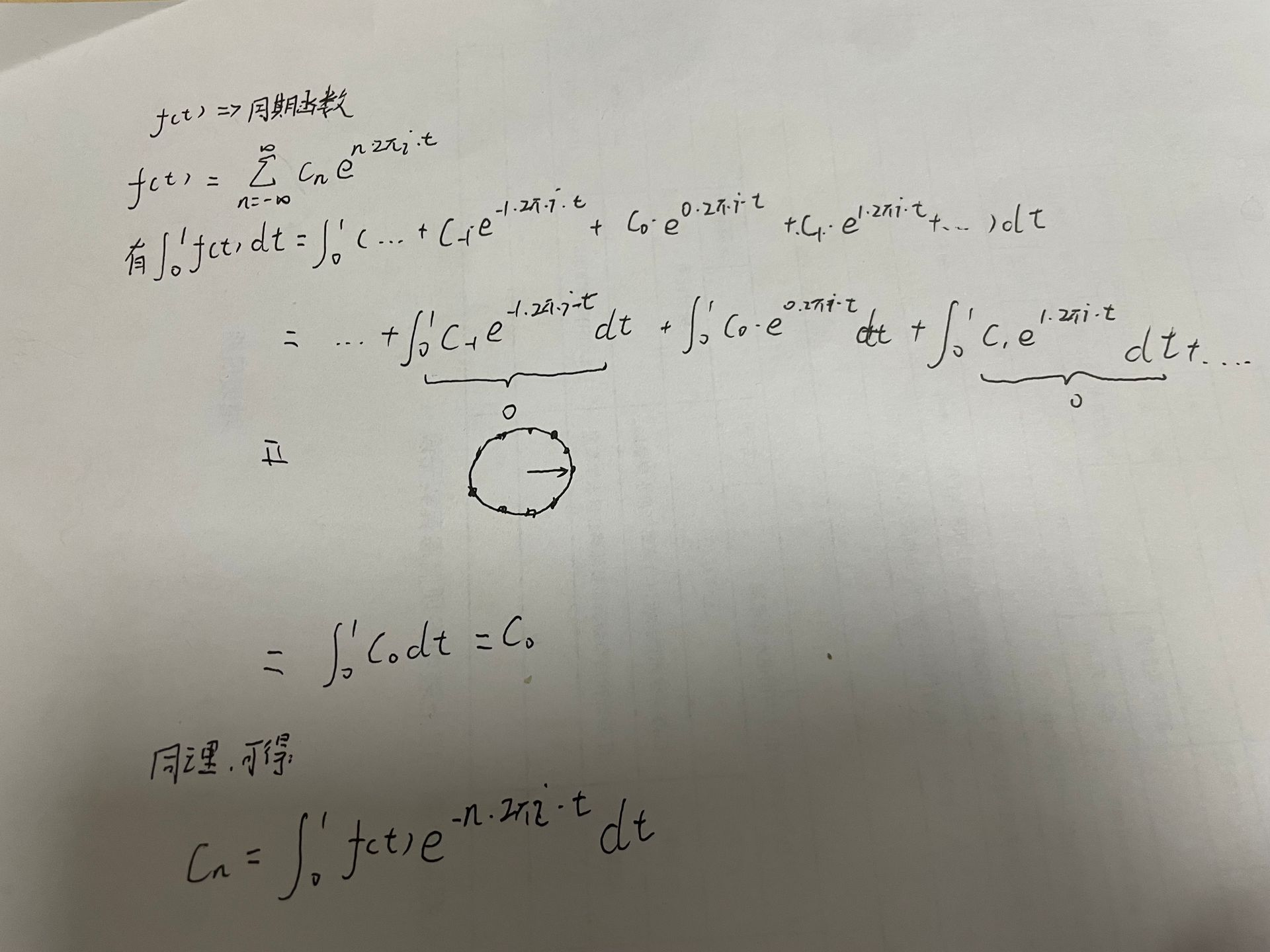
三角函数推导

见这个知乎：

傅里叶系列（一）傅里叶级数的推导

$$f(t)=\frac{1}{2}{a}_0+\sum _{k=1}^{\infty }(a_k\cos 2\pi kt+b_k\sin 2\pi kt)$$

Discrete Fourier Transform(DFT)

$$\{f_1,f_2,f_3,\cdots ,f_n\}\stackrel{\text{DFT}}{\Rightarrow }\{\widehat{f_1},\widehat{f_2},\widehat{f_3},\cdots ,\widehat{f_n}\}$$ $$X[k]=\sum _{n=0}^{N-1}x[n]\cdot e^{-\frac{j2\pi kn}{N}}$$ $$\frac{k}{N}\widehat{=}F,n\widehat{=}t$$

Video: Discrete Fourier Transform - Simple Step by Step

Also, when we do DFT, we need to notice Nyquist Limit

Also,we can write DFT in matrix version:

$$\text{make }{\omega }_N=e^{\frac{-2\pi i}{N}}$$

it have:

$$\left[\begin{array}{c}X[0]\\ X[1]\\ X[2]\\ ⋮\\ X[N-1]\end{array}\right]=\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }_N& {\omega }_N^2& \cdots & {\omega }_N^{N-1}\\ 1& {\omega }_N^2& {\omega }_N^4& \cdots & {\omega }_N^{2(N-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }_N^{N-1}& {\omega }_N^{2(N-1)}& \cdots & {\omega }_N^{(N-1{)}^2}\end{array}\right]\left[\begin{array}{c}x[0]\\ x[1]\\ x[2]\\ ⋮\\ x[N-1]\end{array}\right]$$

For $X[k]$, it means a $\cos$ wine like this:

Fast Fourier transform(FFT)

FFT is a computationally efficient way of computing the DFT

The time complexity of FFT is $O(n\log n)$, and the time complexity of DFT is $O(n^2)$

for DFT:

$$\hat{f}=\underset{\text{DFT Matrix}}{\underbrace{F_{1024}}}\cdot f$$

Z transform

The Z-transform (ZT) is a mathematical tool which is used to convert the difference equations in time domain into the algebraic equations in z-domain.

通常，Z变换有两种类型，unilateral (or one-sided) and bilateral (or two-sided)

bilateral:

$$Z[x(n)]=X(z)=\sum _{n=-\infty }^{\infty }x(n)z^{-n}$$

unilateral:

$$Z[x(n)]=X(z)=\sum _{n=0}^{\infty }x(n)z^{-n}$$

where, z is a complex variable and it is given by:

$$z=r{e}^{j\omega }$$

The unilateral or one-sided z-transform is very useful because we mostly deal with causal sequences. Also, it is mainly suited for solving difference equations with initial conditions.

Fourier Pairs

fourier_pairs.pdf

Reference

• But what is the Fourier Transform? A visual introduction.
• But what is a Fourier series? From heat flow to drawing with circles | DE4
• 傅里叶系列（一）傅里叶级数的推导
• The Discrete Fourier Transform (DFT)
• The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?
• Euler’s formula
• https://www.andreinc.net/2024/04/24/from-the-circle-to-epicycles