History
Chebyshev polynomials
Objective
切比雪夫多项式(Chebyshev Polynomials)是19世纪俄国数学家彼得·切比雪夫(Pafnuty Chebyshev)在19世纪中期引入的,这些多项式具有广泛的应用,并在数学和工程领域中发挥着重要的作用。
切比雪夫多项式的发明主要有以下几个意义和目的:
-
逼近论和插值: 切比雪夫多项式在逼近论和插值中具有重要作用。它们是一组正交多项式,可以用来逼近和插值函数。在逼近论中,人们可以使用切比雪夫逼近将复杂的函数用一组切比雪夫多项式的有限和来表示,这对于数值计算和数据分析非常有用。使用第一类chebyshev多项式的根,也被叫做chebyshev节点来进行多项式插值,可以降低龙格现象,并且提供多项式在连续函数的最佳一致逼近
-
最小二乘法: 切比雪夫多项式在最小二乘法中有广泛的应用。由于它们的正交性质,它们能够提供最小二乘逼近的有效工具。在拟合实验数据或解决非线性最小二乘问题时,切比雪夫多项式可以作为基函数。
-
数值分析: 切比雪夫多项式在数值分析中用于构建有效的数值方法,特别是在数值积分和微分方程的数值解法中。它们的性质使得在数值计算中可以更精确地处理一些数学问题。
-
波动现象: 切比雪夫多项式在研究振动和波动现象中也发挥了重要的作用。它们出现在许多物理学和工程学的问题中,特别是在描述周期性运动和振动的情况下。
Definition
Chebyshev多项式来自于以下两个Chebyshev微分方程的解,
这类方程的解为幂级数,,且系数据有递推关系,
因此我们得到第一类切比雪夫多项式和第二类切比雪夫多项式
第一类切比雪夫多项式
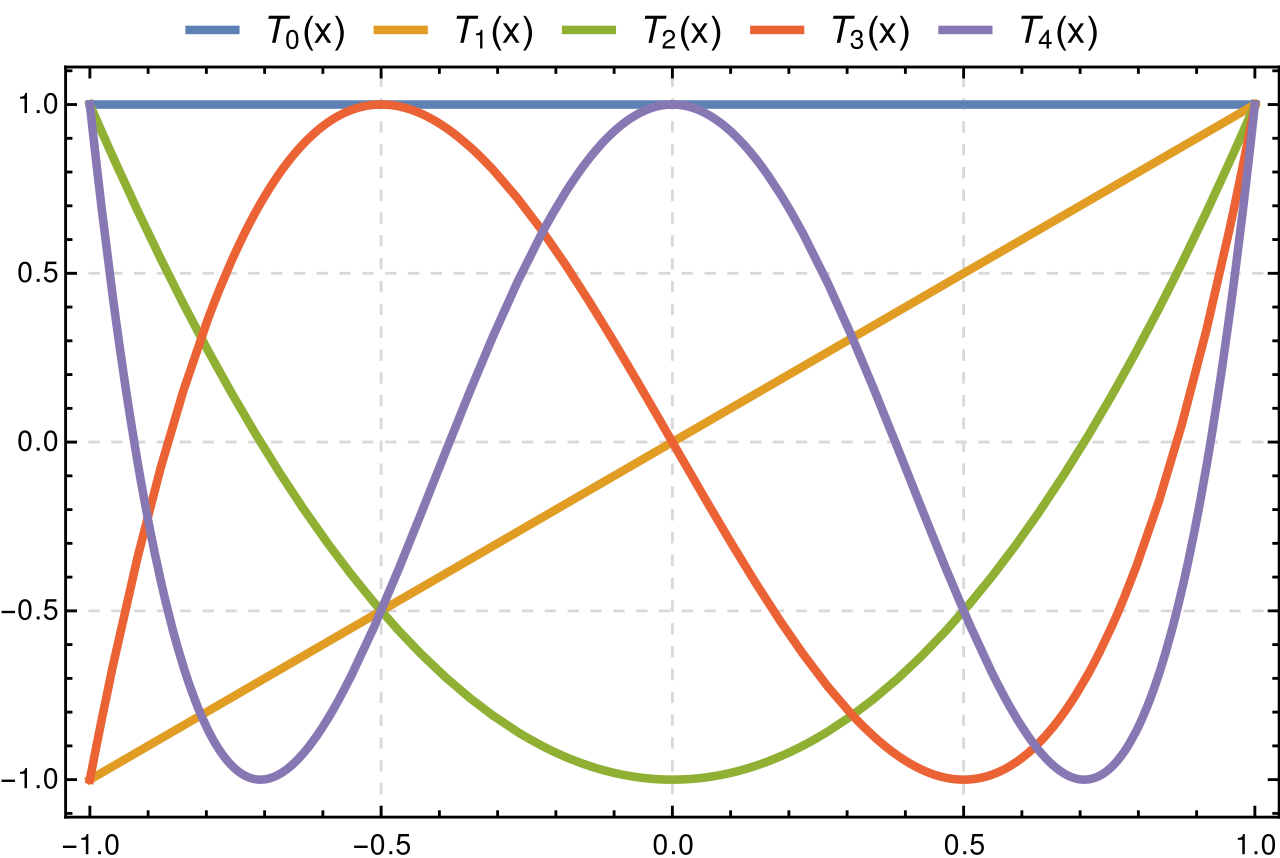
第二类切比雪夫多项式
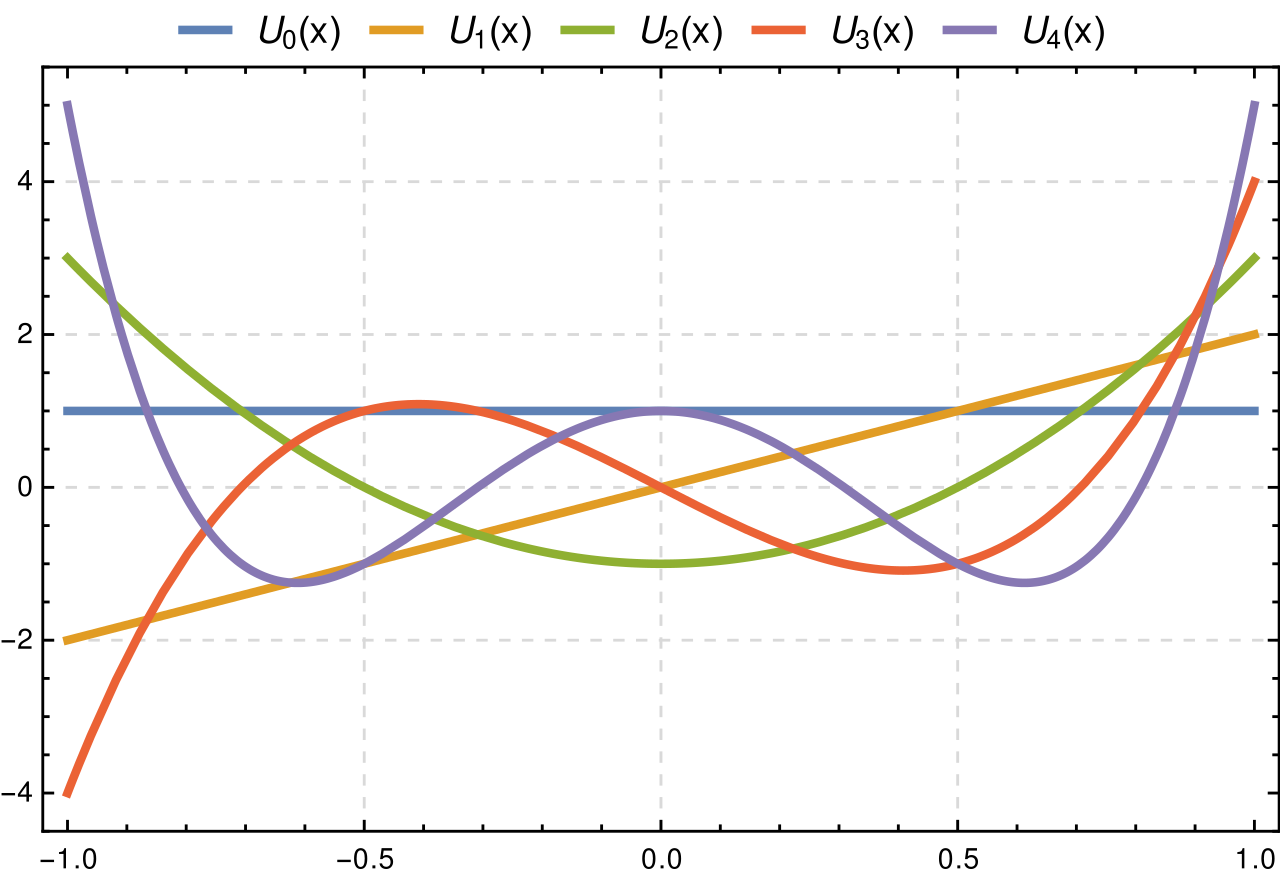
正交性
Chebyshev Root
两类的_n_次切比雪夫多项式在区间[−1,1]上都有_n_ 个不同的根, 称为切比雪夫根, 有时亦称做切比雪夫节点 ,因为是多项式插值时的 插值点 。
的个根为:
的个根分别是:
Chebyshev Filter
Type I Chebyshev Filter
The gain response:
- - ripple factor
- - cutoff frequency
- - Chebyshev polynomial