飞行时间测算

Plan A - 使用Group Delay测算飞行时间

Group Delay

在电信和信号处理领域，群时延（group delay）通常是指信号通过系统时所引起的相位变化与信号频率之间的关系。群时延可以用来描述系统对不同频率信号的相位响应，尤其在宽带通信系统中很有用。

计算群时延的一种常见方法是通过相位对频率的导数。具体地说，对于一个复数传输函数H(f)，其相位为φ(f)，群时延τ可以通过以下公式计算：

$$\tau (f)=-\frac{d\varphi (f)}{df}$$

得到的结果

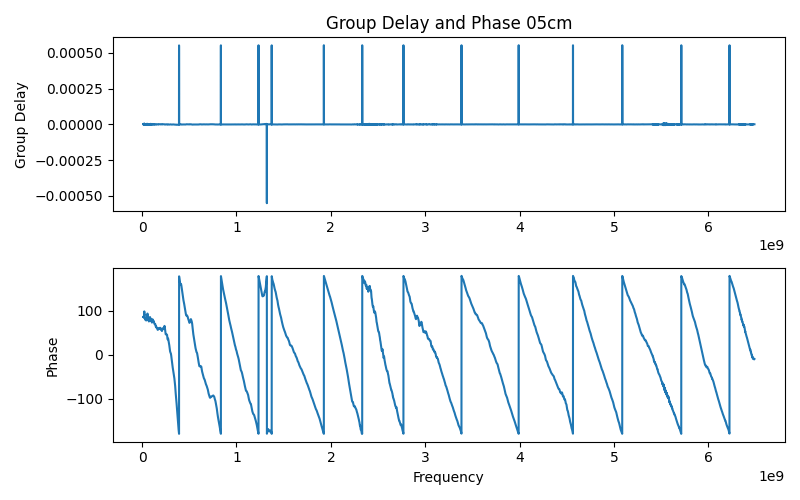
可以看出来，因为相位变换存在着拐点，所以计算得到的group delay在拐点处的导数计算会出现问题，因此我们需要对拐点处的导数计算采取特殊的处理，本次使用的方法是直接对Group Delay的曲线使用中值滤波排除这些拐点的特异值

特异值排除方法：

def sp_detect(signal, window_size=5):
    
    for i in range(window_size, len(signal) - window_size):
        
        window_mean = 0
        
        for j in range(i - window_size, i):
            window_mean += abs(signal[j])
    
        for j in range(i + 1, i + window_size + 1):
            window_mean += abs(signal[j])
            
        window_mean = window_mean / (2 * window_size)
        
        replace_mean = 0 
        
        for j in range(i - window_size, i):
            replace_mean += signal[j]
            
        for j in range(i + 1, i + window_size + 1):
            replace_mean += signal[j]
            
        replace_mean = replace_mean / (2 * window_size)
        
        if abs(signal[i]) > 3 * window_mean:
            
            signal[i] = replace_mean
        
    return signal

排除特异点后，得到的结果如下图：

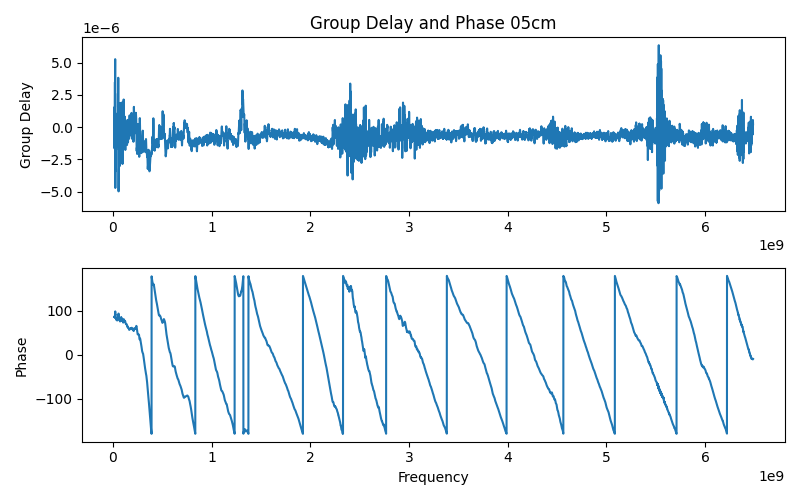
然后我们取Group Delay的曲线的中位数并减去耦合信号的Group Delay中位数当作本距离下的Delay time，画出Delay time和距离的关系如下：

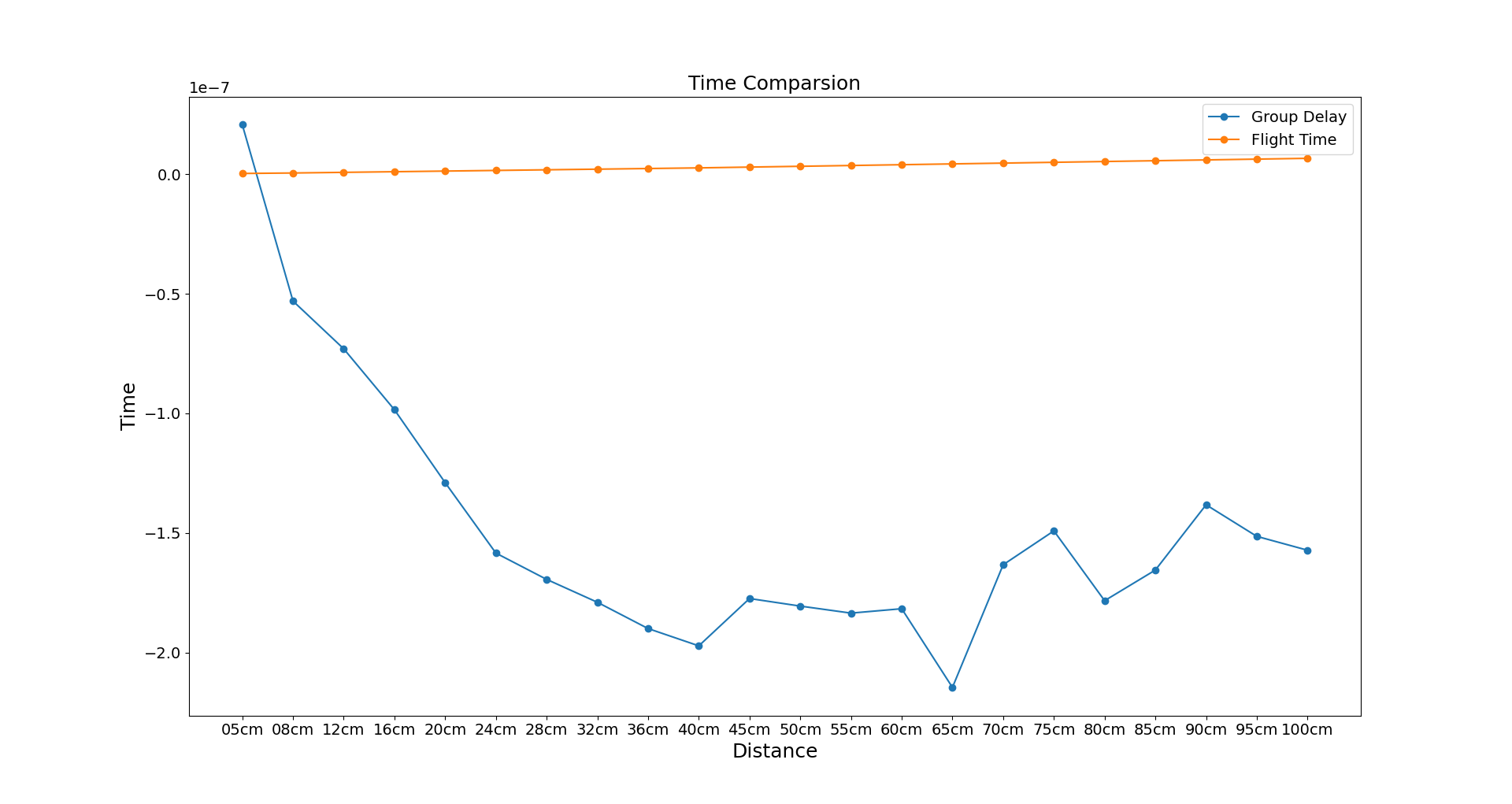
可以看出来，从Group Delay的路线方法来得到飞行时间的测算方案并没有行得通，这可能的原因有以下几点：

1. 多路径和多模式： 如果系统存在多条传输路径或多个传输模式，群时延可能会受到这些因素的影响。
2. 相位不稳定性： VNA测量中的相位信息可能会受到测量系统中的相位不稳定性的影响，这可能影响群时延的准确性。
3. 非线性效应： 在某些情况下，非线性效应可能导致信号频率的变化，从而影响相位。
4. 群延时和飞行时间关系理解仍不到位，并且算法处理可能并不科学

准备改进的点：

1. 使用窗函数聚焦于特定频段下的群延时，目前尚不清楚是群延时曲线稳定处可以体现飞行时间还是在出现干扰处可以体现

Plan B - 考察单一频段下相位变化估算飞行时间

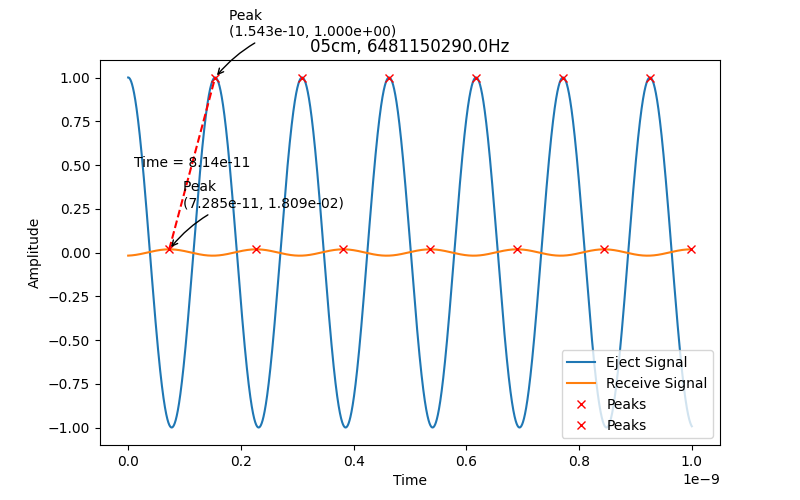
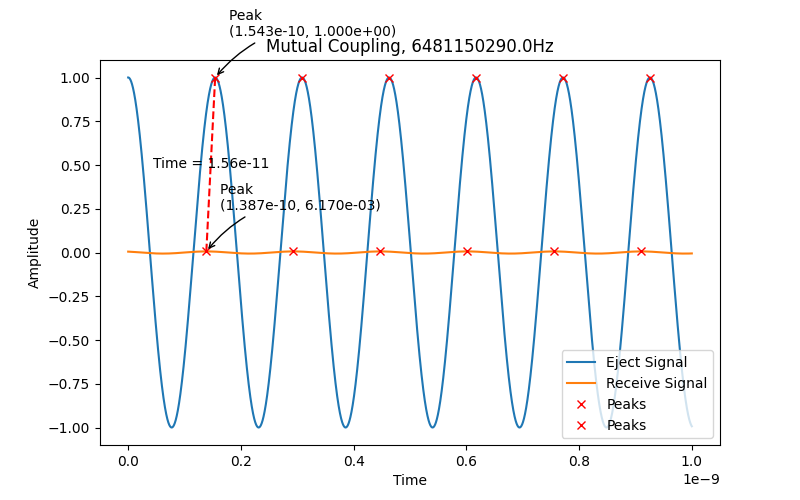
以mutual coupling signal为基准来计算飞行时间，最终得到的结果：

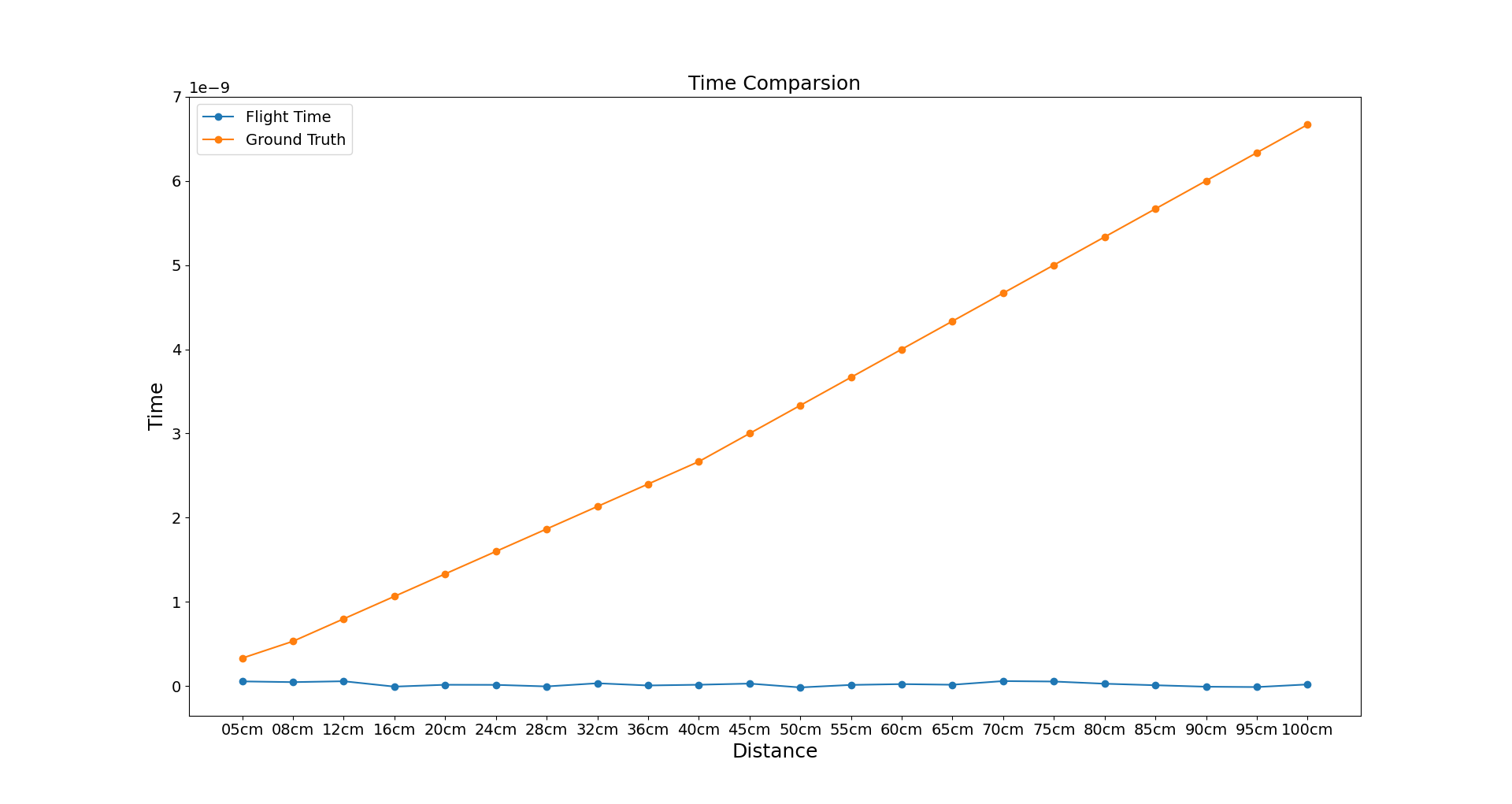
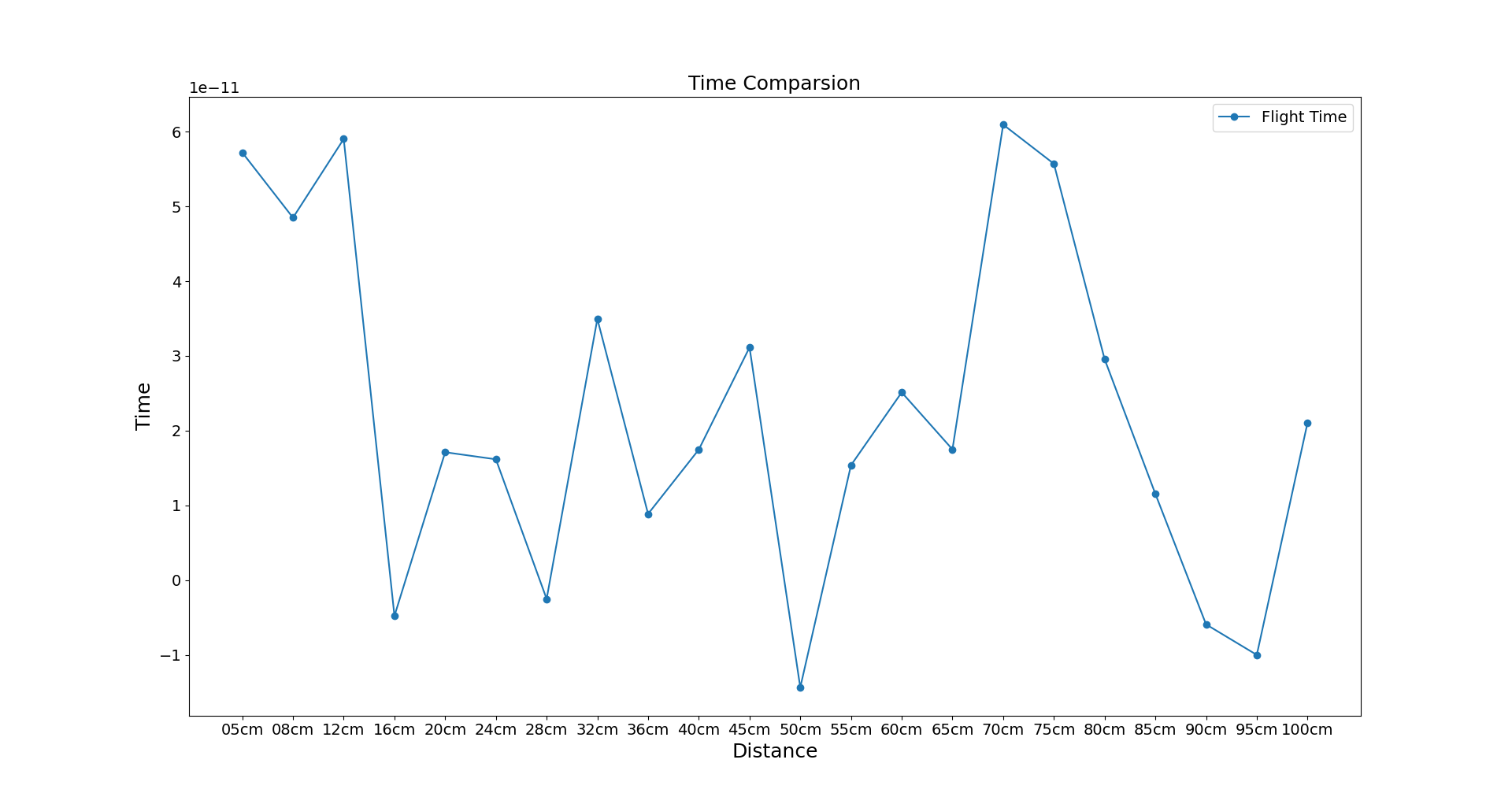
这个方法还需要继续完善，同时方案一导致的误差对这个方案的影响是相同的