问题
高频信号细节过于丰富导致传统Hilbert变换求包络的结果过于贴合曲线,使得变化趋势没有得到有效简化
包络求解方法
本次任务使用的包络求解方法基于MATLAB envelope函数,其方法一共有三种:
Hilbert变换
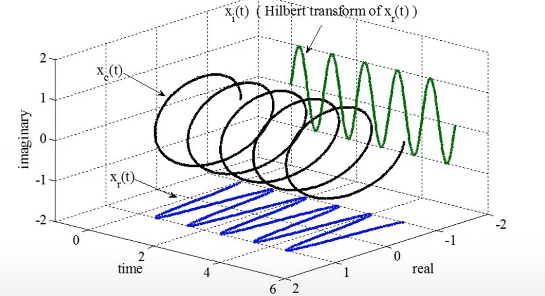
analytical = hilbert(signal)
envelope = abs(analytical)Hilbert变换将实信号变换为分析信号来研究信号的瞬时振幅和瞬时相位,其可以画出非常贴合曲线的包络,这个方法没有参数可以调节,效果如下:
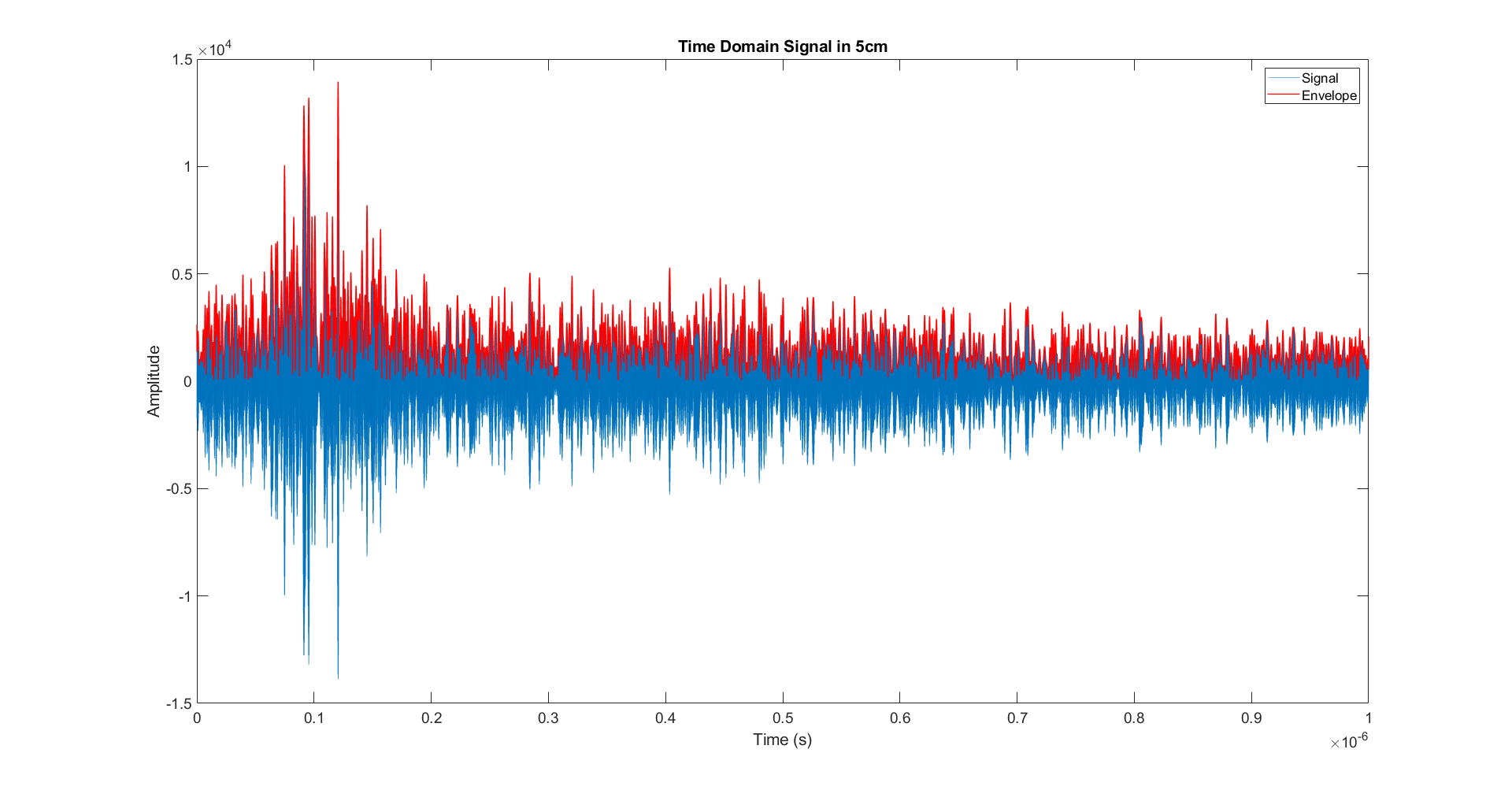
放大细节图如下:
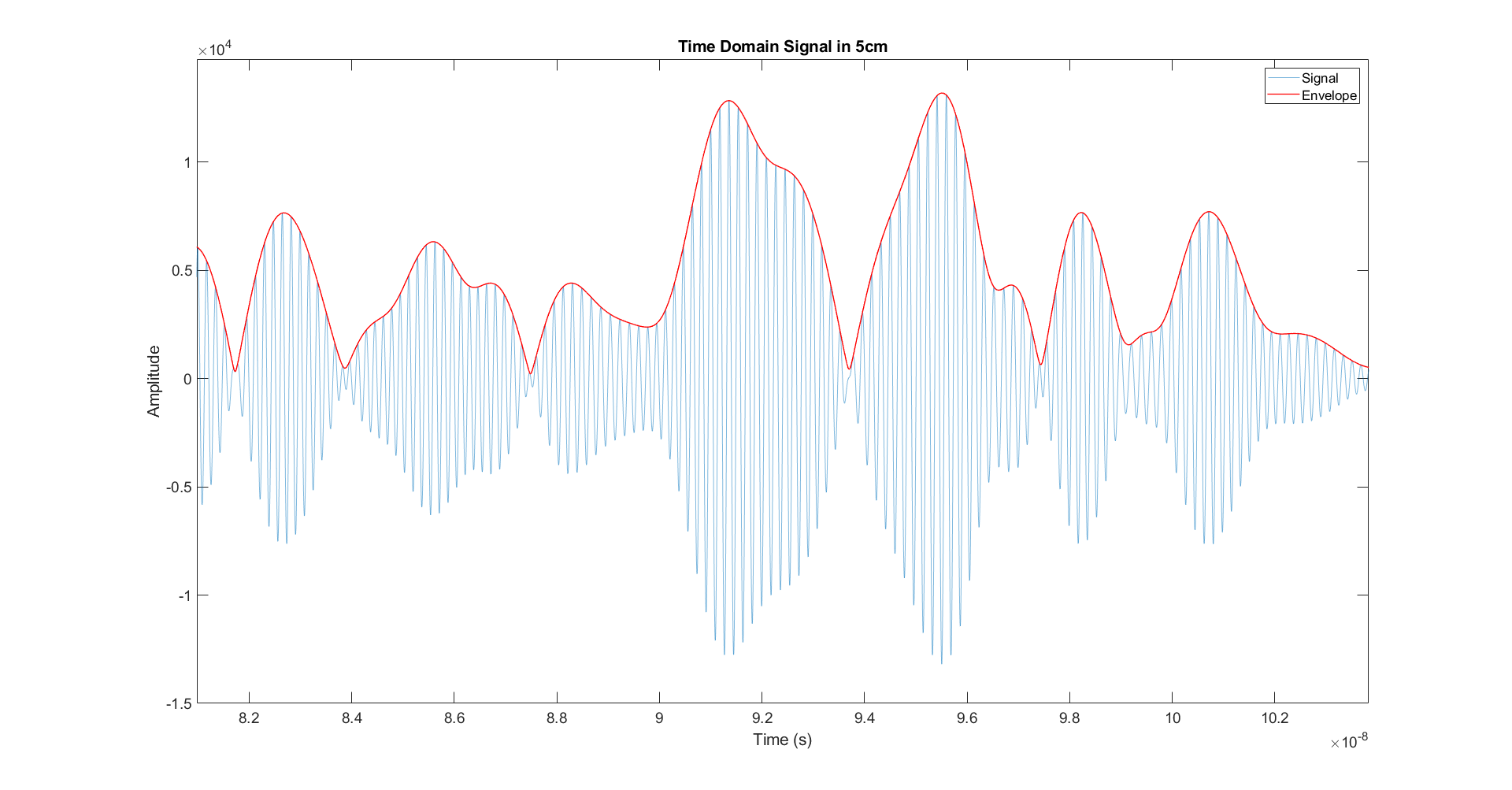
其结果在细节处处理的包络效果良好,但是从宏观图景上并没有很好
Hilbert Filter
[yupper, ylower] = envelope(x, fl, 'analytic')Hilbert Filter的方法是用长度为 fl (filter length) 的希尔伯特 FIR 滤波器对 x 进行滤波,计算出解析信号,这样的方法可以使得包络更加贴合曲线细节变化,随着fl的增大,结果越来越接近于Hilbert变换的方法,不符合我们的需求,效果如图:
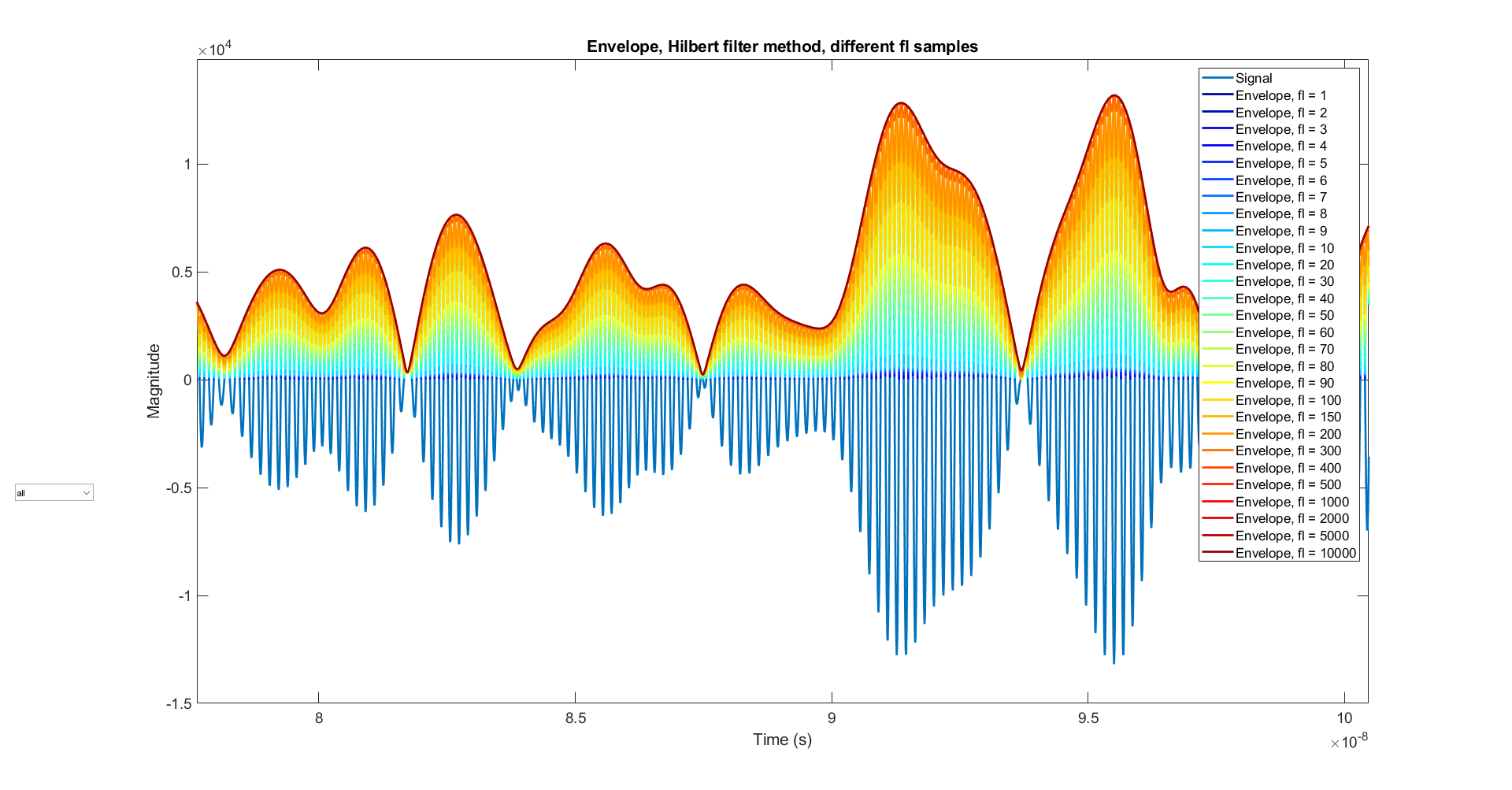
RMS
RMS(Root Mean Square)是一种用于测量信号能量的方法,它可以用于音频处理中的各种应用,包括音频信号的包络提取。RMS包络表示信号在一段时间内的均方根值,通常用于衡量信号的整体能量而不受信号的波形变化影响。
RMS包络的计算步骤如下:
- 平方:对信号的每个样本值进行平方运算。
- 平均: 对平方后的值进行平均操作,通常是对一定时间窗口内的值进行平均。
- 开方:对平均值进行开方运算,得到均方根值。
滑动窗口后得到RMS包络;
[yupper, ylower] = envelope(x, wl, 'rms')MATLAB使用RMS法求包络时,窗口之间的重叠量参数并不可以调节
其结果如下:
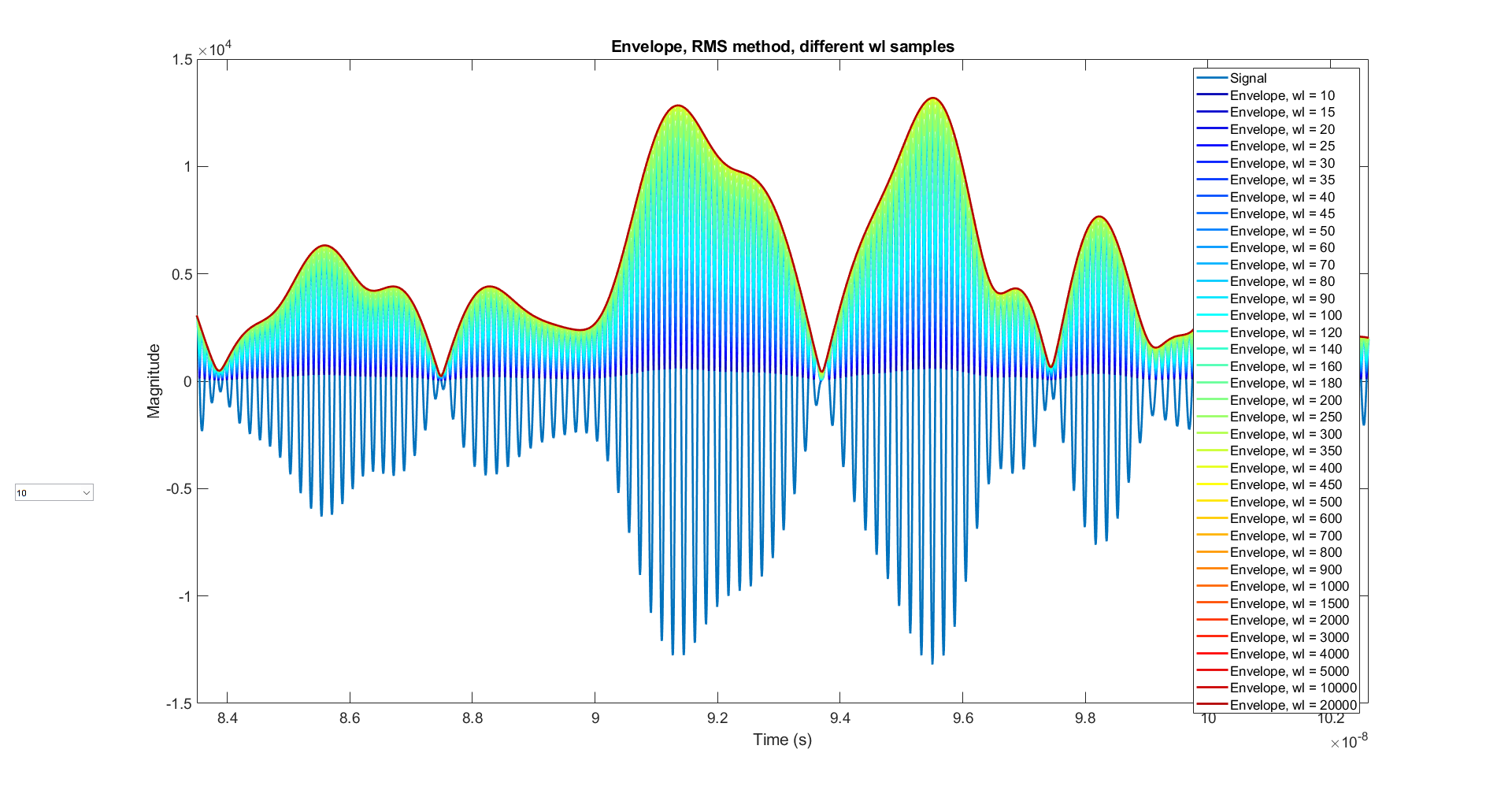
结果显示,随着RMS的窗口越长,其结果越接近于Hilbert变换算法,其结果仍然不满足我们的需求。
Peaks
[yupper, ylower] = envelope(x, np, 'peak')这个方法包络线是通过对至少相隔 np 个样本的局部最大值进行样条插值确定的。
测试不同np参数对我们结果的影响:
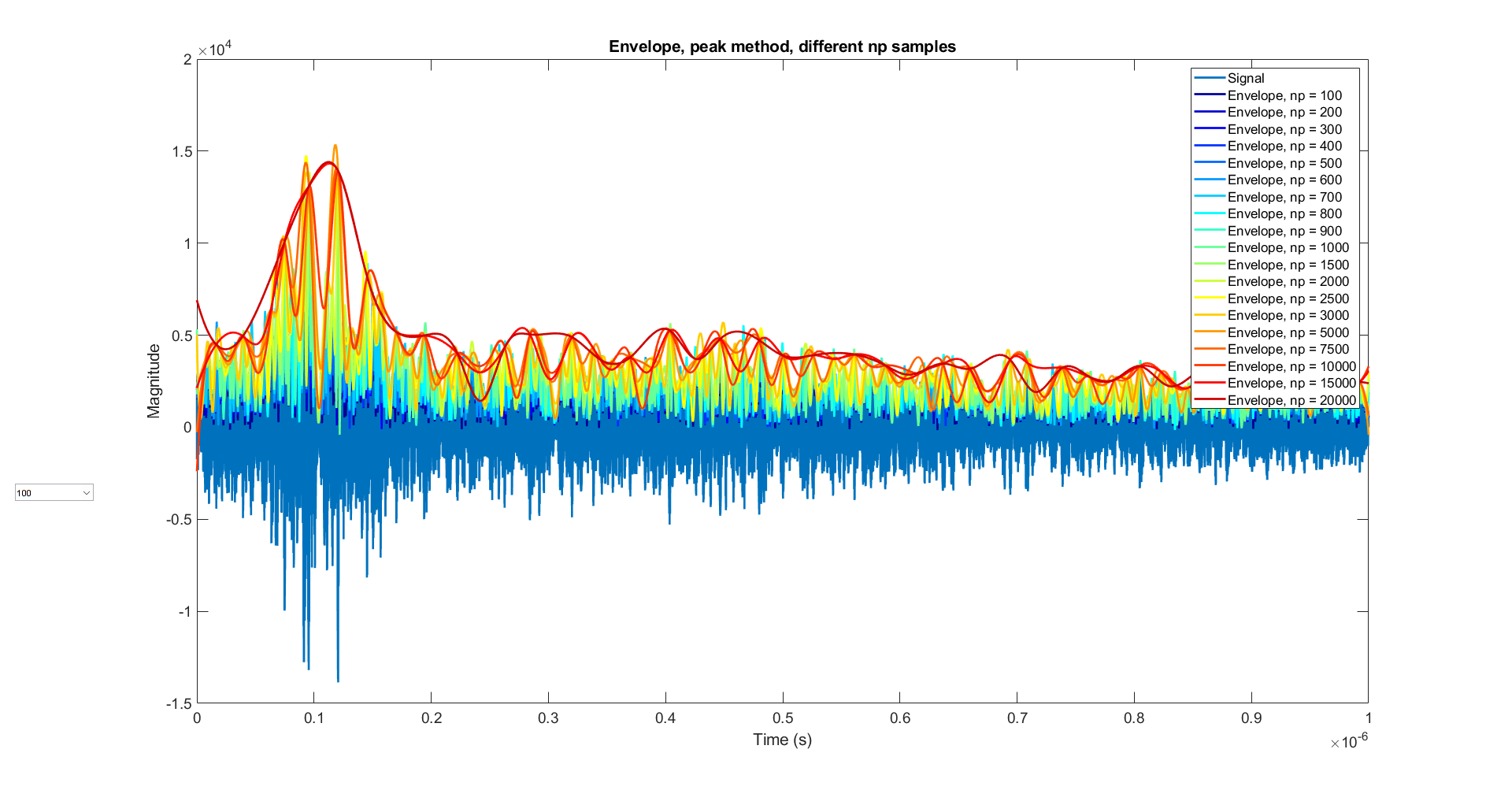
显然,Peaks的算法非常简单直白,随着np的增大,包络会越来越粗线条。这个方案可能可以解决我们的问题。
Hilbert变换 + 低通滤波器
在Hilbert变换的基础上,调节低通滤波器截止频率和阶数这两个参数来达到较为良好的平滑效果,如下:
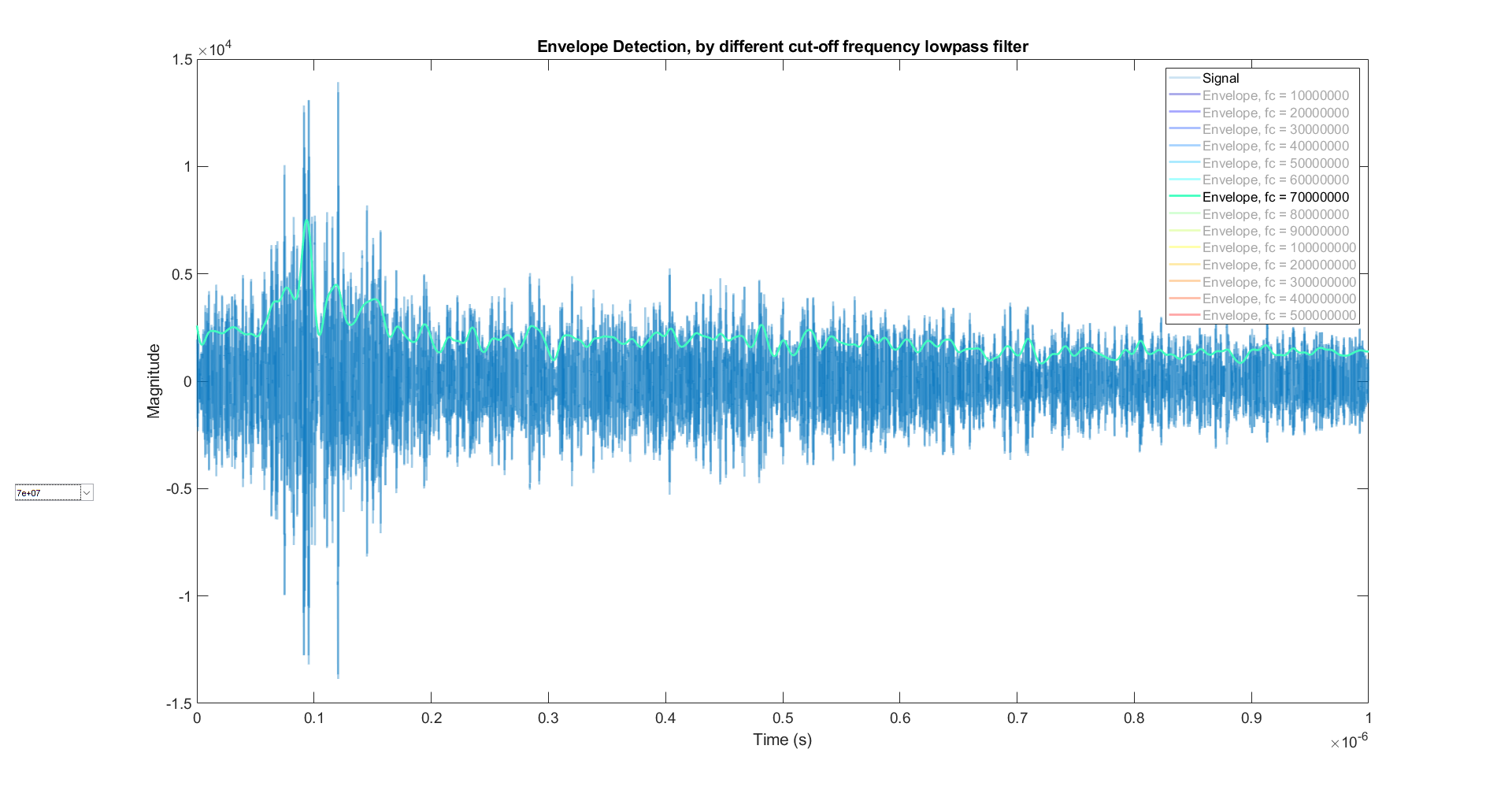
这个包络方法也可能对我们找到关键点有帮助
结论
后续通过以上方法计算包络后,按照峰值点作为时间计算关键点去计算时间差,来求得距离,但是结果仍然出现错误。