Maxwell's Equation

Equation

$$\nabla \cdot E=\frac{\rho }{{ϵ}_0}$$ $$\nabla \cdot B=0$$ $$\nabla \times E=-\frac{\partial B}{\partial t}$$ $$\nabla \times B={\mu }_0(J+{ϵ}_0\frac{\partial E}{\partial t})$$

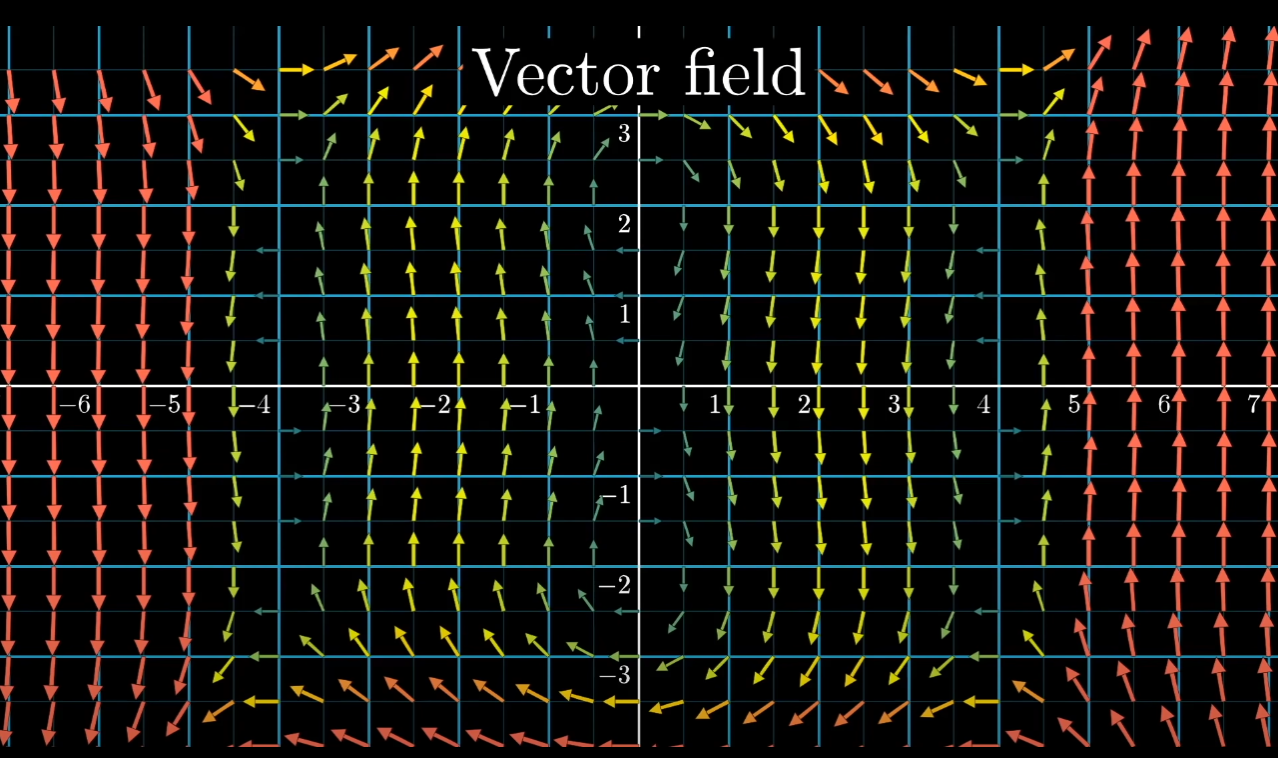
Vector field

Essentially a vector field is what you get if you associate each point in space with a vector, some magnitude and direction. Maybe those vectors represent the velocities of particles of fluid at each point in space or maybe they represent the force of gravity at many different points in space or maybe a magnetic field strength.

Note

If you were to draw the vectors to scale, the longer ones end up just cluttering the whole thing, so it’s common to basically lie a little and artificially shorten ones that are too long. Maybe using color to give some vague sense of length.

Divergence

Divergence $\cdot$ Vector filed是来衡量在(x, y)点你产生fluid的能力

所以上述图中，产生fluid的source点，他们的Divergence $\cdot$ Vector filed是positive的

那些fluid流入的sink端，他们的Divergence $\cdot$ Vector filed就是negative的

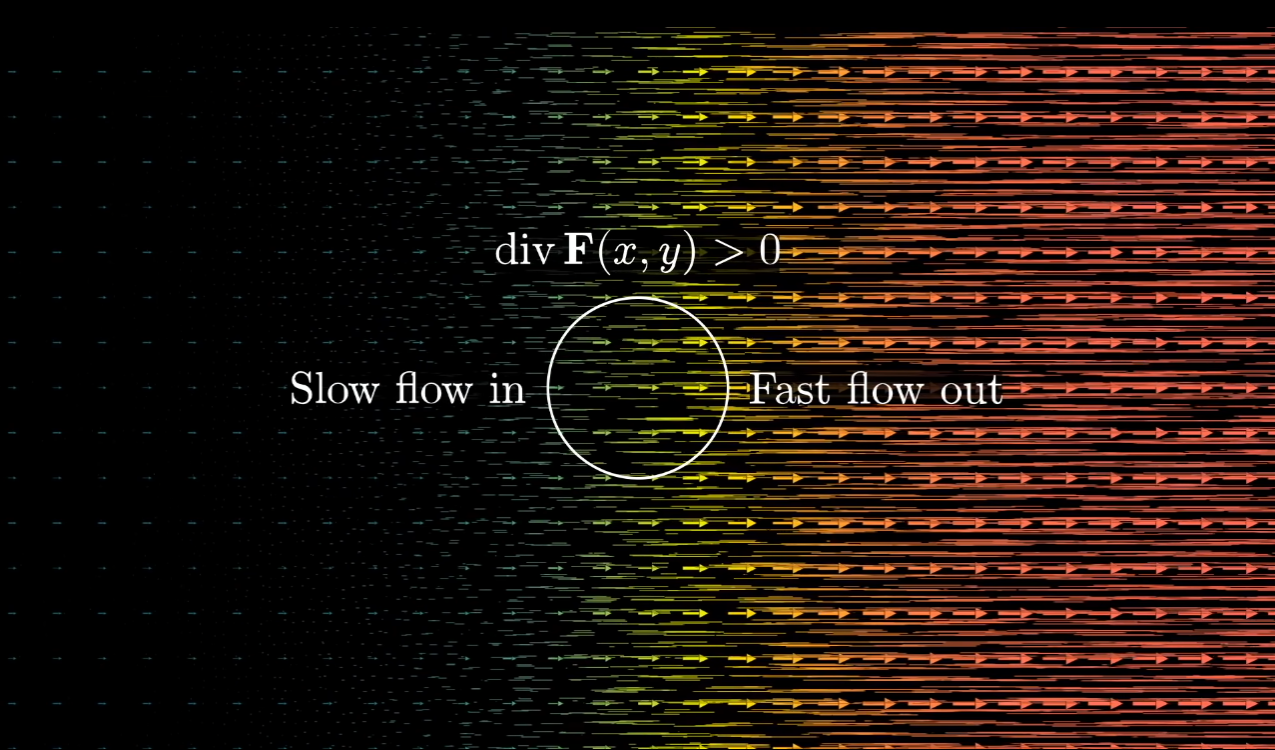
同时，如果点可以slow flow in变fast slow out，这个点位的divergence $\cdot$ vector filed也是positive的

Vector field input point得到的是一个多维的输出，指向一个方向并带有scale；divergence $\cdot$ vector field，它的输出depends on the behavior of the field in small neighborhood around that point。输出为一个数值，衡量这个point acts as a source or a sink

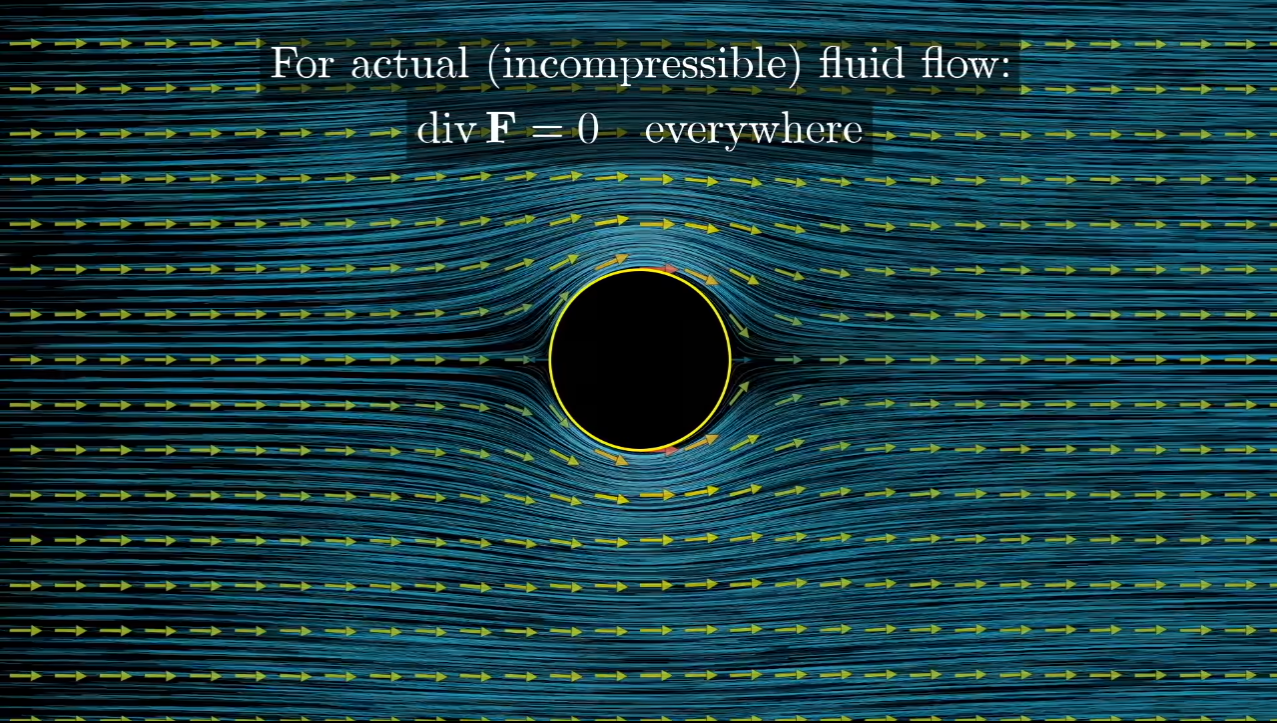
Note

For actual fluid flow: $\text{div}F=0$ everywhere

Curl

Curl是衡量fluid在point被rotate的程度，clockwise方向是positive curl，counterclockwise是negative curl。

上图中这个点的curl也是非零的，因为fluid上快下慢，result in clockwise influence

Calculate divergence and curl

$$\text{div}F=\nabla \cdot F=\left[\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\end{array}\right]\cdot \left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}$$ $$\text{curl}F=\nabla \times F=\left[\begin{array}{c}\frac{\partial }{\partial x}\\ \frac{\partial }{\partial y}\end{array}\right]\times \left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=\frac{\partial F_y}{\partial x}-\frac{\partial F_x}{\partial y}$$

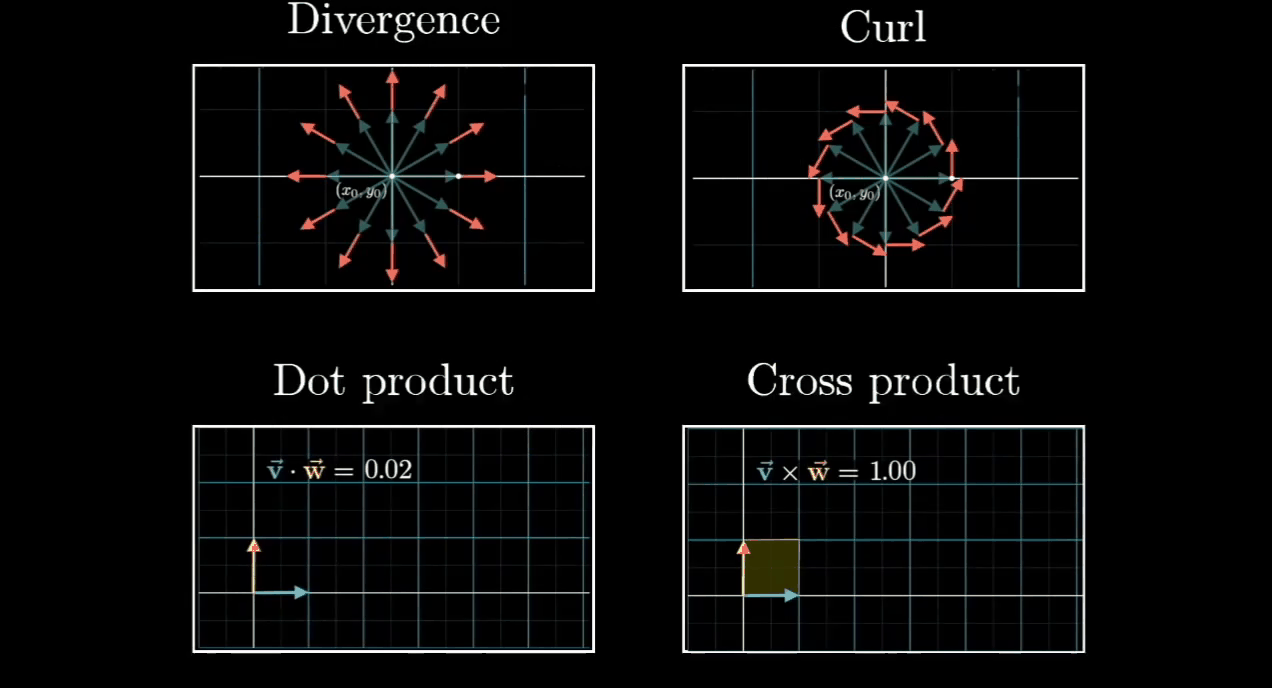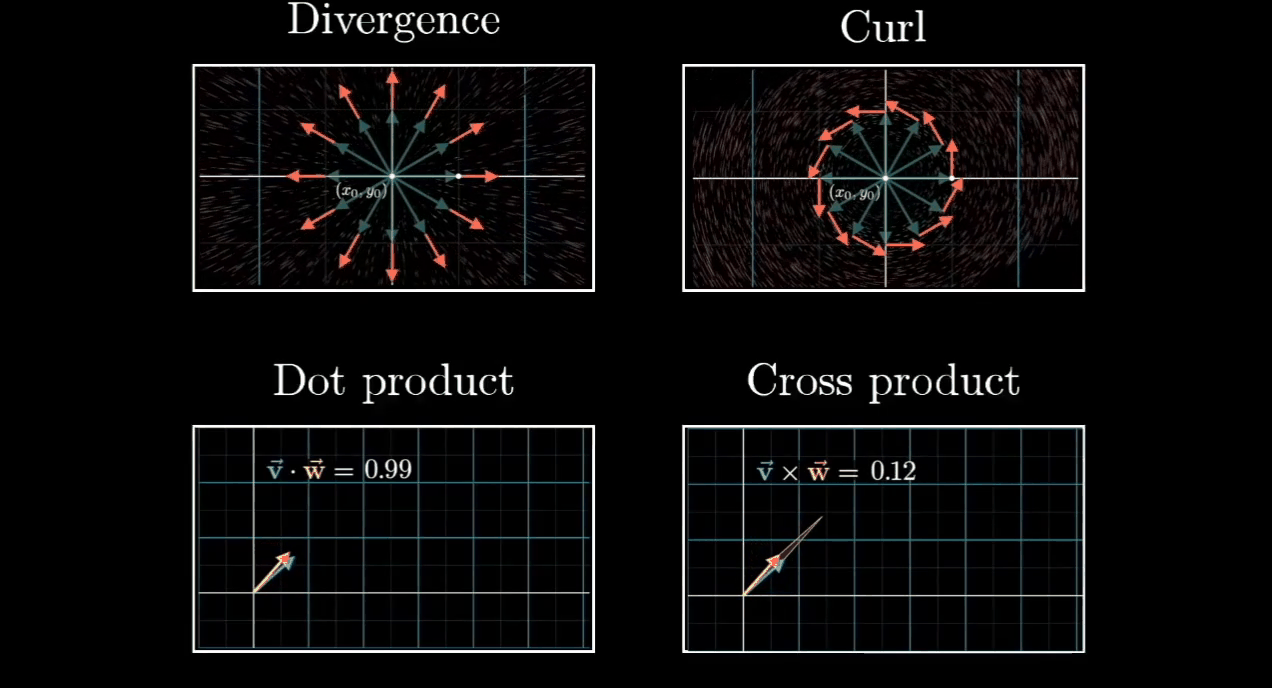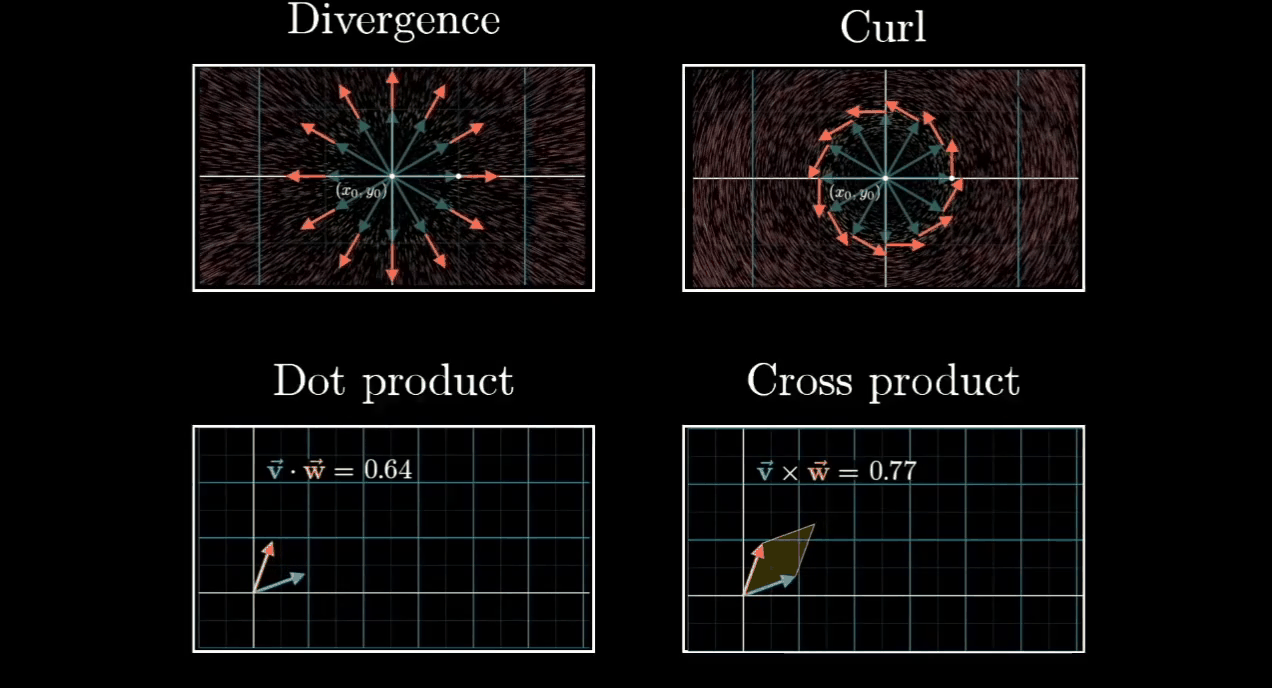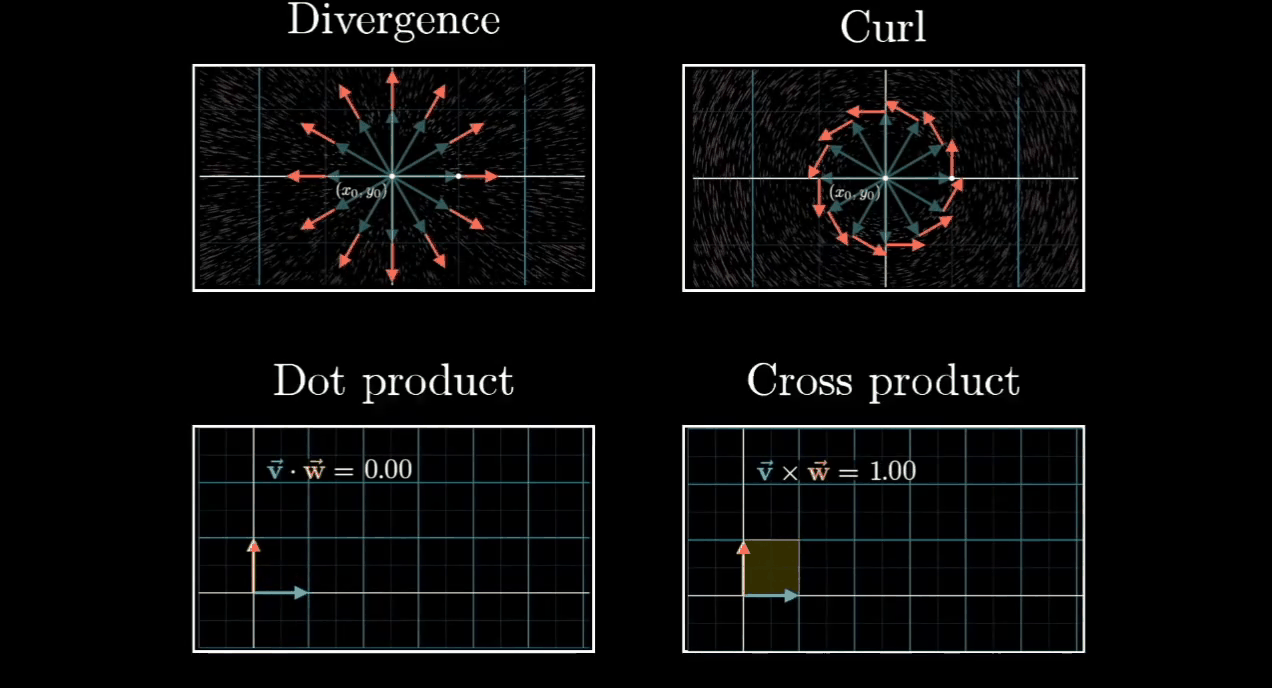
Detail Explanation

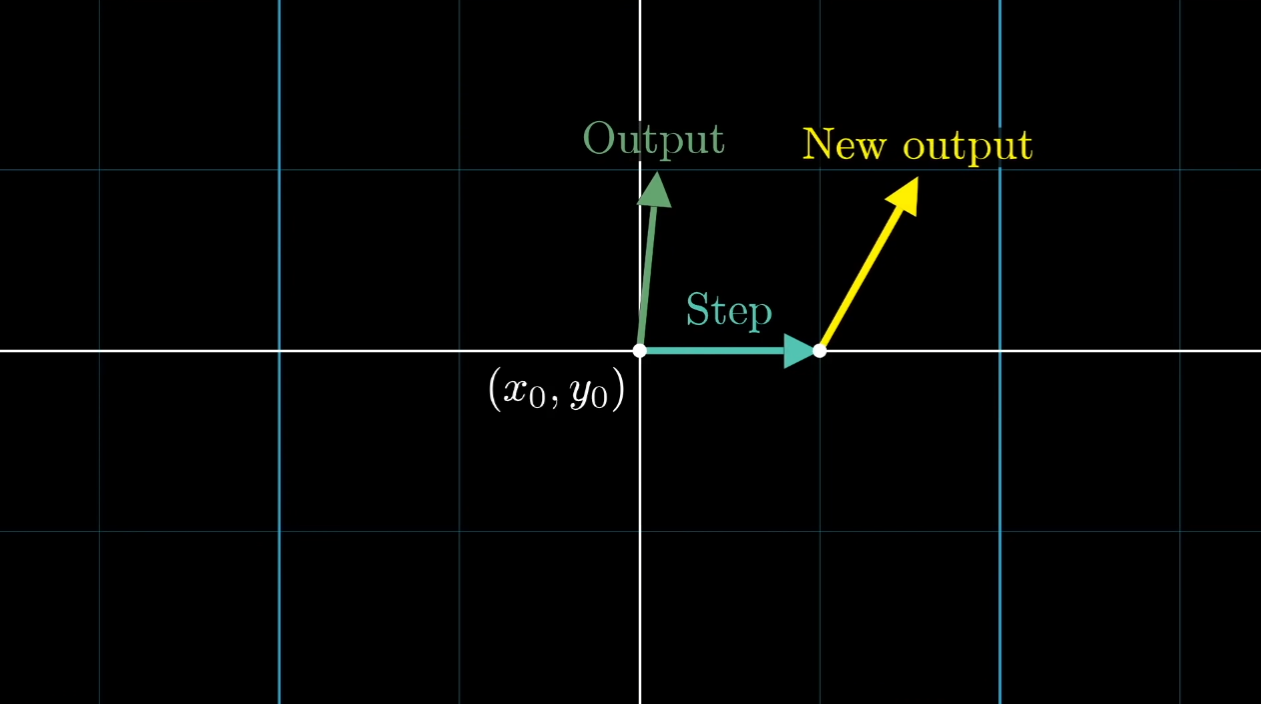
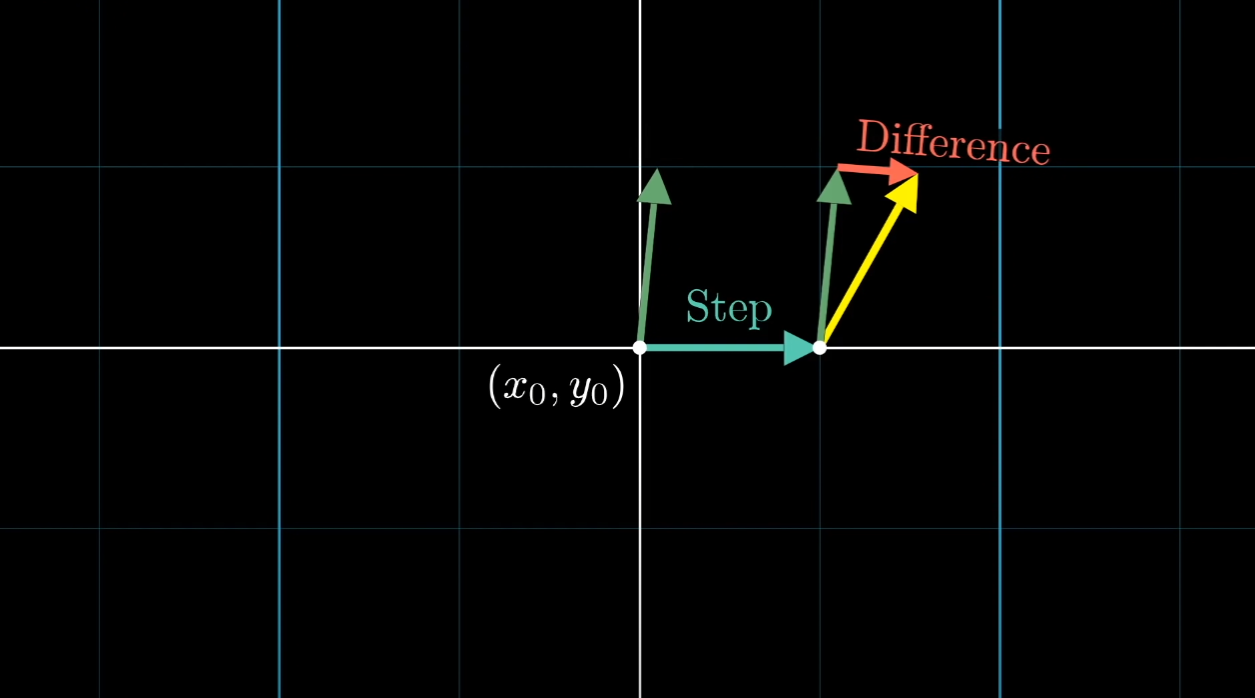
在$(x_0,y_0)$微分一个很小的tiny step，会有一个新的vector，它与原有的vector会有一个difference。

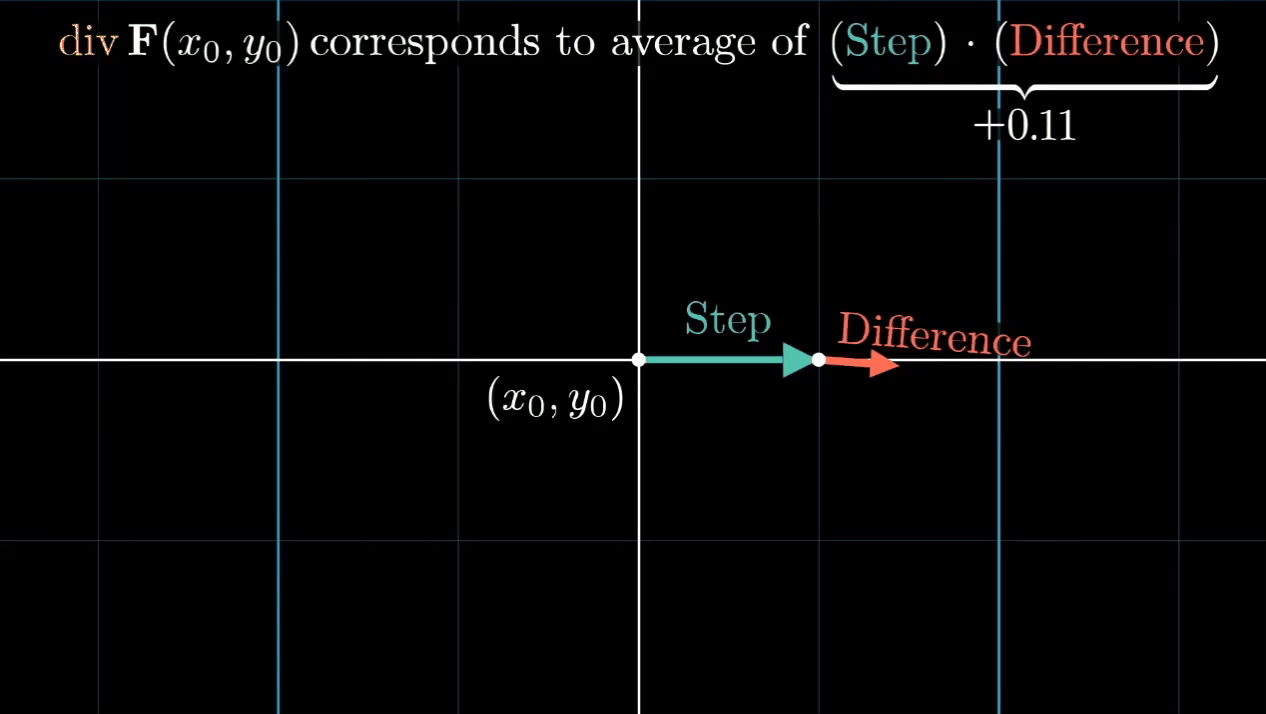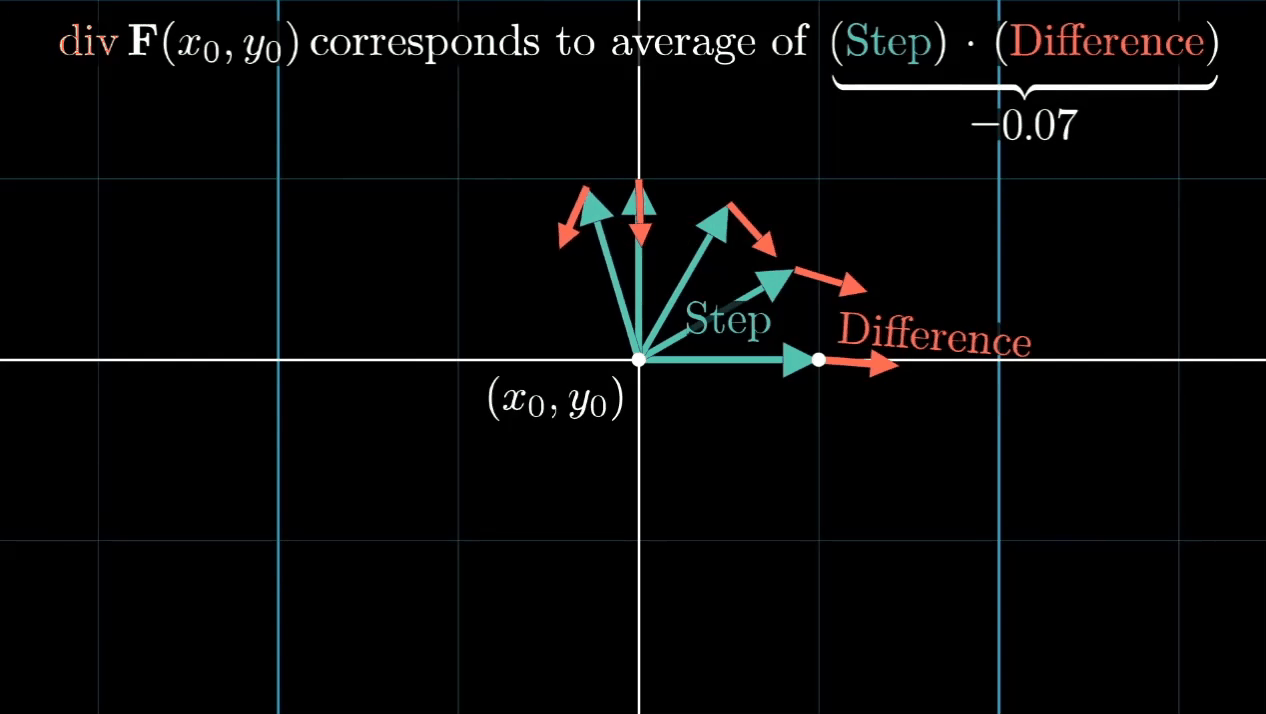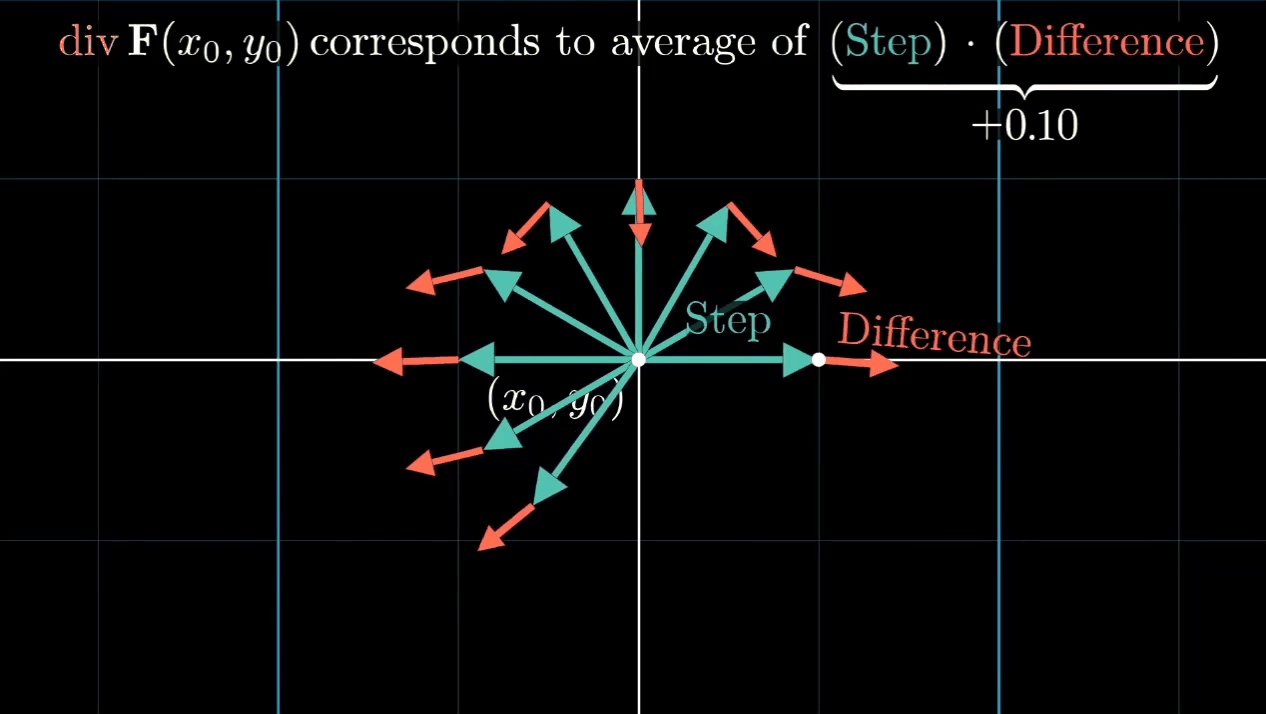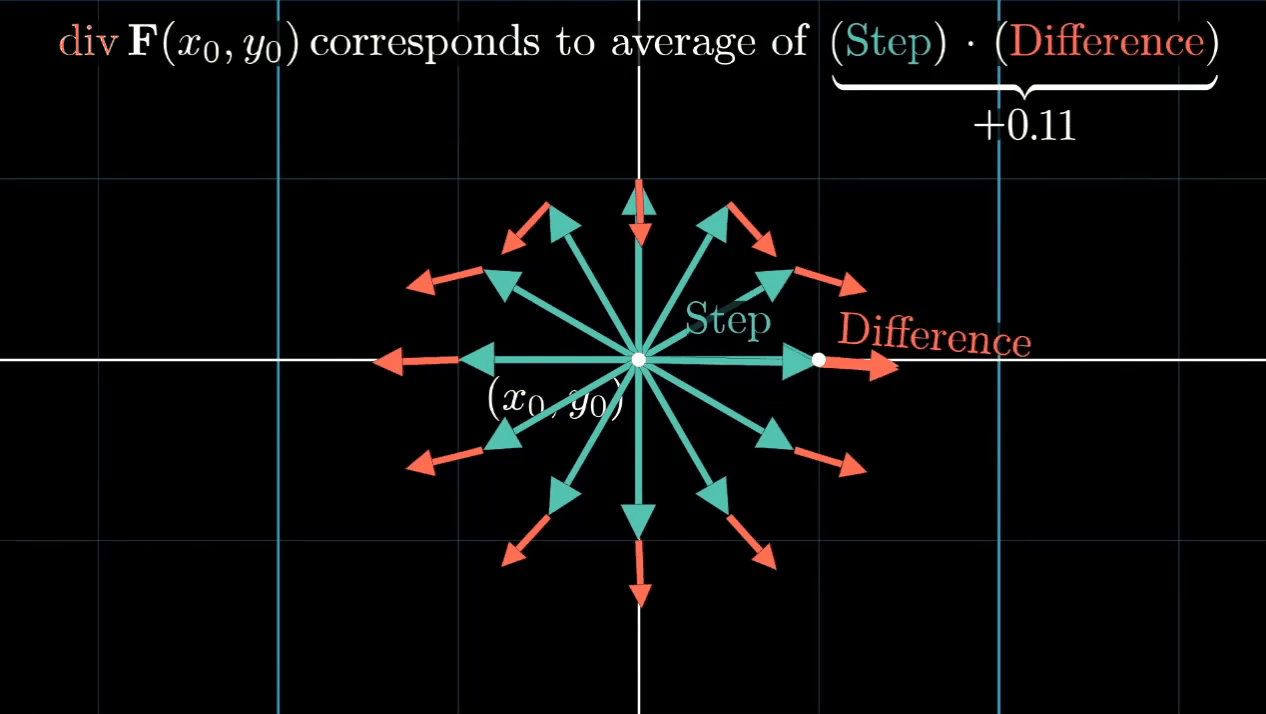
$\text{div}F(x_0,y_0)$其实就是corresponds to $360^{\circ }$方向的average的Step $\cdot$ Difference

可以想象一个source端，它朝四面发射vector，它的Step $\cdot$ Difference自然就是positive的

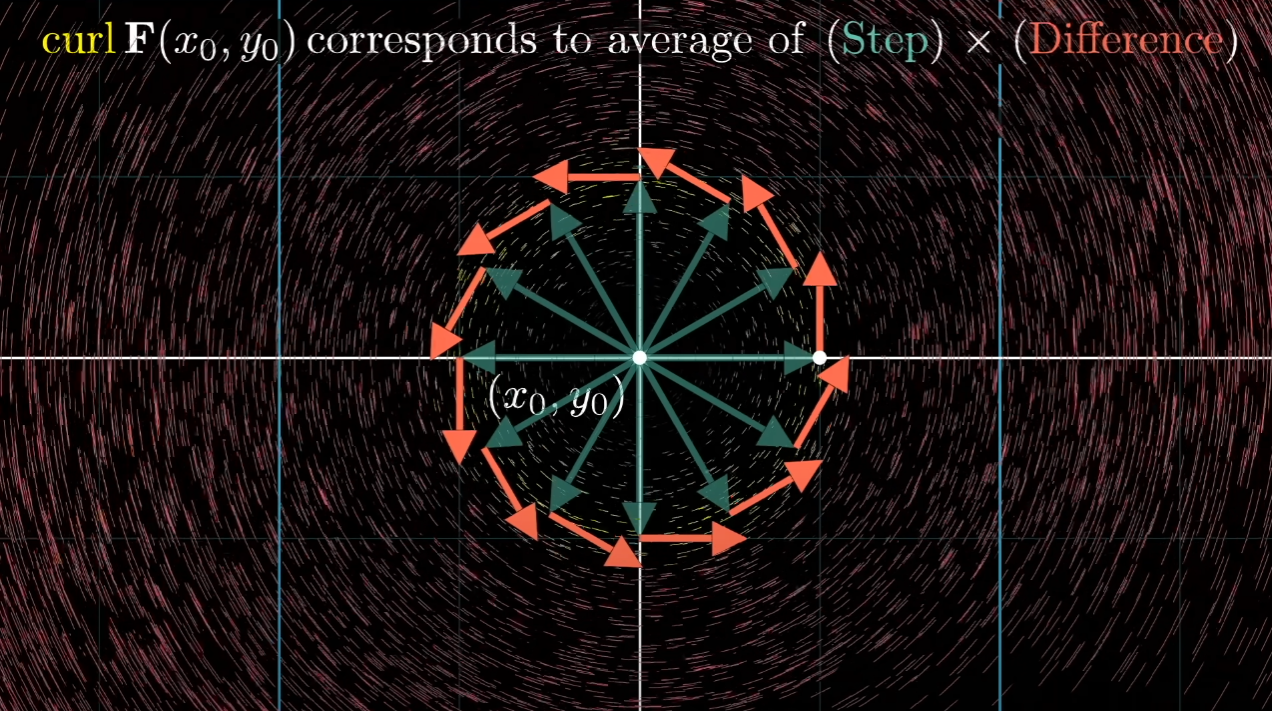
同理，不难想象的是，$\text{curl}F(x_0,y_0)$是corresponds to Step $\times$ Difference

Understand Maxwell’s Equation

学会vector filed中的divergence和curl，是理解Maxwell’s Equation的关键

Gauss’s Law

$$\text{div}E=\frac{\rho }{{ϵ}_0}$$

• $\rho$是charge density
• ${ϵ}_0$是Epsilon Naught，free space的介电常数，它决定free space空间中电场的强度

Note

形象的

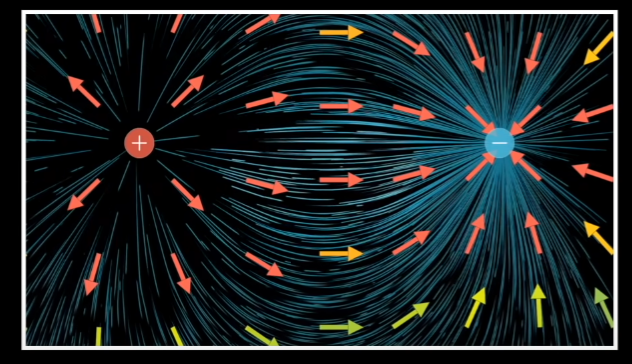
Gauss’s law stating that divergence of an electric field at a given point is a proportional to the charge density at that point.

Positively charged regions as acting like sources of some imagined fluid and negatively charged regions as being the sinks of that fluid.

Parts of space where there is on charge the fluid would be flowing incompressively just like water.

Gauss’s law for magnetism

$$\text{div}B=0$$

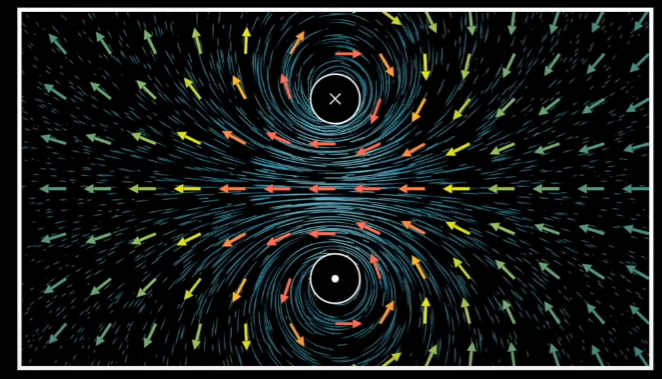
磁场的divergence在任意地方为0，说明磁场的fluid是incompressible的，没有source也没有sinks，就像water一样。也有这样的interpretation，说明magnetic monopoles是不存在的

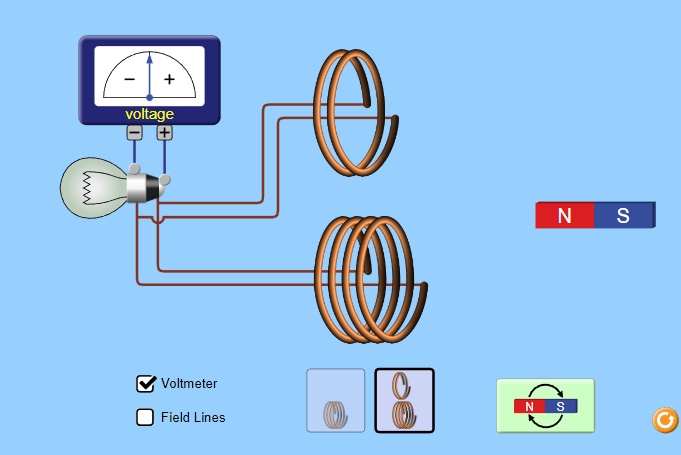
Maxwell–Faraday equation (Faraday’s law of induction)

$$\nabla \times E=-\frac{1}{c}\frac{\partial B}{\partial t}$$

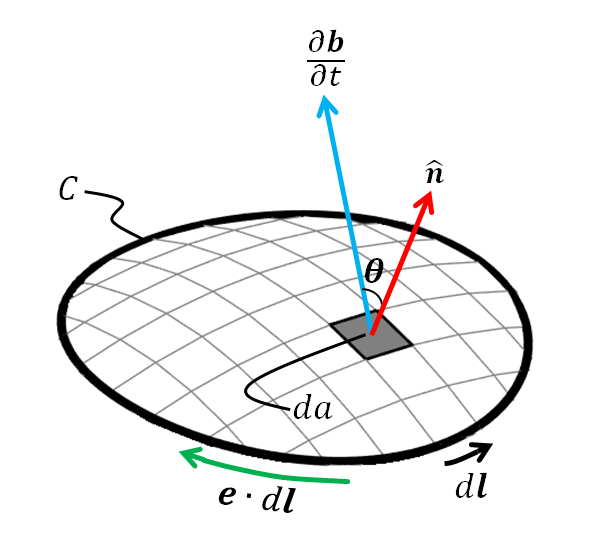
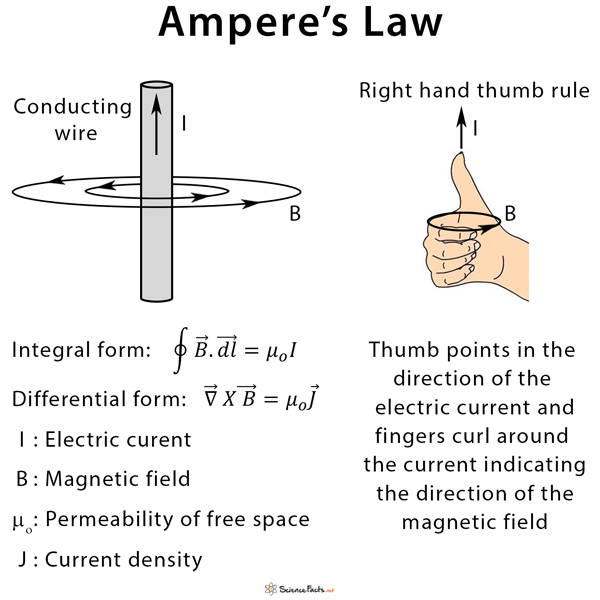
Ampère’s circuital law (with Maxwell’s addition)

$$\nabla \times B=\frac{1}{c}(4\pi J+\frac{\partial E}{\partial t})$$

Maxwells equation explain EM wave

Maxwells的完备对称理论表明，电场力和磁力并不是分开的，而是同一事物——电磁力的不同表现形式。 这种力的经典统一是当前试图统一自然界中四种基本力——引力、电力、强核力和弱核力——的动机之一。

Maxwells从Maxwells equation中预测了EM wave的存在。

Maxwells意识到振荡电荷，就像交流电路中的电荷一样，会产生变化的电场。 他预测这些变化的场会像跳跃的鱼在湖上产生的波浪一样从源头传播。

麦克斯韦预测的波将由振荡电场和磁场组成——定义为电磁波（EM 波）。 电磁波能够对距其源很远的电荷施加力，因此它们可能是可检测的。 Maxwells通过求解Maxwells方程组，可以求出EM的速度$c$，

$$c=\frac{1}{\sqrt{{\mu }_0{ϵ}_0}}=3\times 10^{8}m/s$$

电磁波的波段处于无法被肉眼观测的波段，直到Maxwells去世后，才被Hertz用实验证实了电磁波的存在。

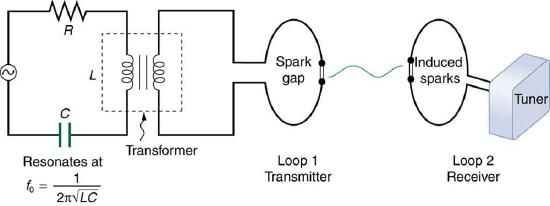
Reference

• Fun fluid-flow illustrations - by 3B1B
• Divergence and curl: The language of Maxwell’s equations, fluid flow, and more - YouTube vedio by 3b1b
• Let There Be Light: Maxwell’s Equation EXPLAINED for BEGINNERS - YouTube vedio by Parth G
• Faraday’s Law - online experiment
• # Maxwell’s Equations- Electromagnetic Waves Predicted and Observed