⭐⭐The significance test tells us whether or not what we observe in the sample is expected to be true in the population, and can be conducted through a hypothesis test.⭐⭐
Goal⭐
• The sample correlation coefficient () between x and y is known (can be computed using samples) • The population correlation coefficient () between x and y is unknown (because we only have sample data) • Goal: We want to make an inference about the value of based on
Hypothesis Test
The hypothesis test will let us infer whether the value of the population correlation coefficient is close to 0 or significantly different from 0. We decide this based on the sample correlation coefficient and the sample size
Situation:
• close to 0: means there is not a significant linear correlation between x and y in the population. • significantly different from 0: means there is a significant correlation between x and y in the population.
For hypothesis test, we have two types - the null and alternative hypotheses.
• The alternative hypothesis is always what we are trying to prove. • The null hypothesis is the hypothesis that we are trying to provide evidence against.
Detailed Explaination
-
零假设(Null Hypothesis) - 通常表示为。 零假设是一个默认的假设,它通常表示没有效应、没有差异或变量之间没有关系。换句话说,零假设通常提出了一个“无效果”的声明,比如两组数据的均值没有差异、两个变量之间没有相关性等。在假设检验中,研究者试图通过收集和分析数据来寻找拒绝零假设的证据。
例如,如果研究者想要检验两种药物对血压的影响是否有差异,零假设可能是“两种药物对降低血压的效果没有差异”。
-
备择假设(Alternative Hypothesis) - 通常表示为或。 备择假设与零假设相对立,它提出了一个“有效果”的声明,即存在效应、差异或关系。备择假设通常是研究者真正感兴趣的假设,它反映了研究者希望证明的效应或关系。
在上述药物对血压影响的例子中,备择假设可能是“两种药物对降低血压的效果存在差异”。
Classic Test Method
Here’s some classic test method:
- T-Test (Student’s T-Test)
- ANOVA (Analysis of Variance)
- Mann-Whitney U Test - MWU (Mann-Whitney U Test)
- Kruskal-Wallis H Test - KW (Kruskal-Wallis H Test)
- Friedman Test - FT (Friedman Test)
- ANCOVA - ANCOVA (Analysis of Covariance)
- Pearson Correlation Coefficient - PCC (Pearson Correlation Coefficient)
- Factor Analysis - FA (Factor Analysis)
- Cluster Analysis - CA (Cluster Analysis)
- Time Series Analysis - TSA (Time Series Analysis)
- … …
T-test
Here we introduce a very classic test method, called T-test, also called Student’s T-test, which is an inferential statistic that allows to test an assumption applicable to a population, or simply, it allows to use sample data to generalize an assumption to an entire population.
Info
T检验是由威廉·戈塞特(William Sealy Gosset)在20世纪初提出的,他使用笔名“Student”发表了相关论文,因此这种检验有时也被称为“Student’s t-test”。它通常用于样本量较小的情况
T-value
Equation:
T值(t-value)是从T检验中得到的统计量,它是样本均值差异与样本内变异性的比率。T值越大,意味着样本均值之间的差异相对于样本内的变异性越大,这通常会导致更低的p值,从而增加了拒绝零假设(即两组均值没有差异)的证据。换句话说,T值越大,我们越有理由相信两组之间的均值差异是真实存在的,而不是由随机变异引起的。
T值的大小并不直接影响相关性的可重复性。然而,如果我们在讨论的是重复测量的均值差异,那么在某种程度上,较大的T值可能会使得研究者更有信心认为这种差异是可靠的,因为较大的T值意味着较小的p值,这可能会使得研究结果在统计上更显著。但是,这并不意味着相关性的可重复性得到了提高,因为相关性的可重复性涉及到的是变量之间关系的一致性,而不是均值差异的显著性。
P-value
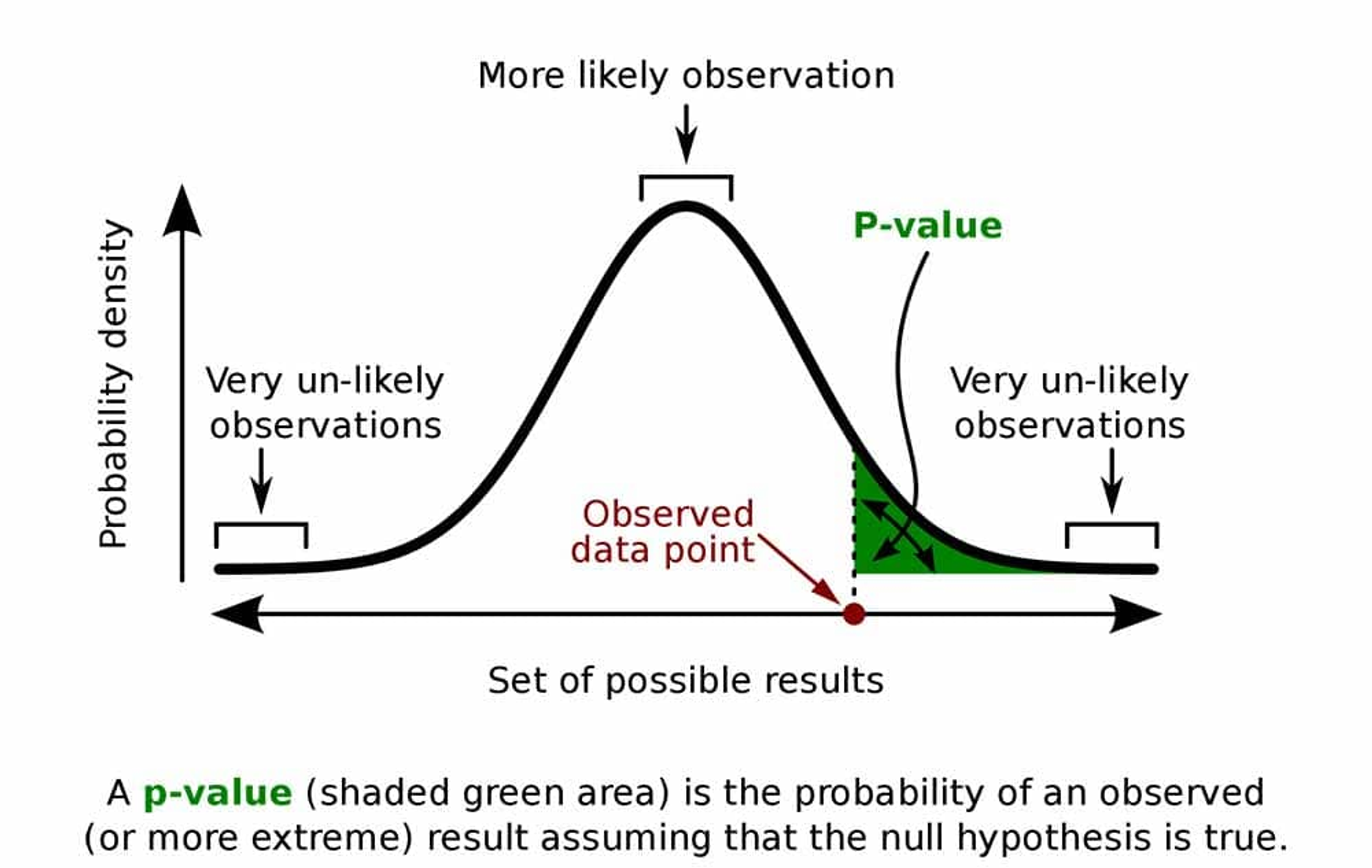
P值(P-value),全称为概率值(Probability value),是统计假设检验中的一个重要概念。它用于帮助我们决定是否拒绝零假设(null hypothesis)。P值衡量的是,在零假设为真的情况下,观察到的统计量(如T值、Z值等)或更极端情况出现的概率。
在进行假设检验时,我们通常设定一个显著性水平(alpha level),常用的值有0.05、0.01等。这个显著性水平是我们事先决定的拒绝零假设的阈值。如果计算出的P值小于这个显著性水平,我们就有理由拒绝零假设,认为观察到的效应或差异是统计上显著的,即不太可能是由随机变异引起的。
例如,假设我们进行一个T检验,零假设是两组数据的均值没有差异。如果我们得到的P值为0.03,而我们设定的显著性水平为0.05,那么P值小于0.05,我们就拒绝零假设,认为两组数据的均值存在显著差异。
需要注意的是,P值并不直接告诉我们零假设是真还是假,也不提供效应大小的信息。它只是表示在零假设成立的前提下,得到当前统计结果或更极端结果的概率。此外,P值也不是与发现效应的大小相关联的概率。一个很小的P值并不意味着效应很大,它只意味着结果不太可能是偶然发生的。
在使用P值时,应该避免一些常见的误解和滥用,如将P值解释为支持备择假设的概率,或者将P值与研究的结论重要性等同起来。正确理解和解释P值对于统计分析的有效性和科学性的结论至关重要。
Conclusion
1、小概率原理:小概率事件在一次试验中是几乎不可能发生的,假若在一次试验中小概率事件事实上发生了。那只能认为该事件不是来自我们假设的总体,也就是认为我们对总体所做的假设不正确。
2、观察到的显著水平:由样本资料计算出来的检验统计量观察值所截取的尾部面积。这个概率越小,反对原假设,认为观察到的差异表明真实的差异存在的证据便越强,观察到的差异便越加理由充分地表明真实差异存在。
3、检验所用的显著水平:针对具体问题的具体特点,事先规定这个检验标准。
4、在检验的操作中,把观察到的显著性水平与作为检验标准的显著水平标准比较,小于这个标准时,得到了拒绝原假设的证据,认为样本数据表明了真实差异存在。大于这个标准时,拒绝原假设的证据不足,认为样本数据不足以表明真实差异存在。
5、检验的操作可以用稍许简便一点的作法:根据所提出的显著水平查表得到相应的值,称作临界值,直接用检验统计量的观察值与临界值作比较,观察值落在临界值所划定的尾部内,便拒绝原假设;观察值落在临界值所划定的尾部之外,则认为拒绝原假设的证据不足。