Transformer in LLM

Architecture

图1: 原始Transformer模型架构图

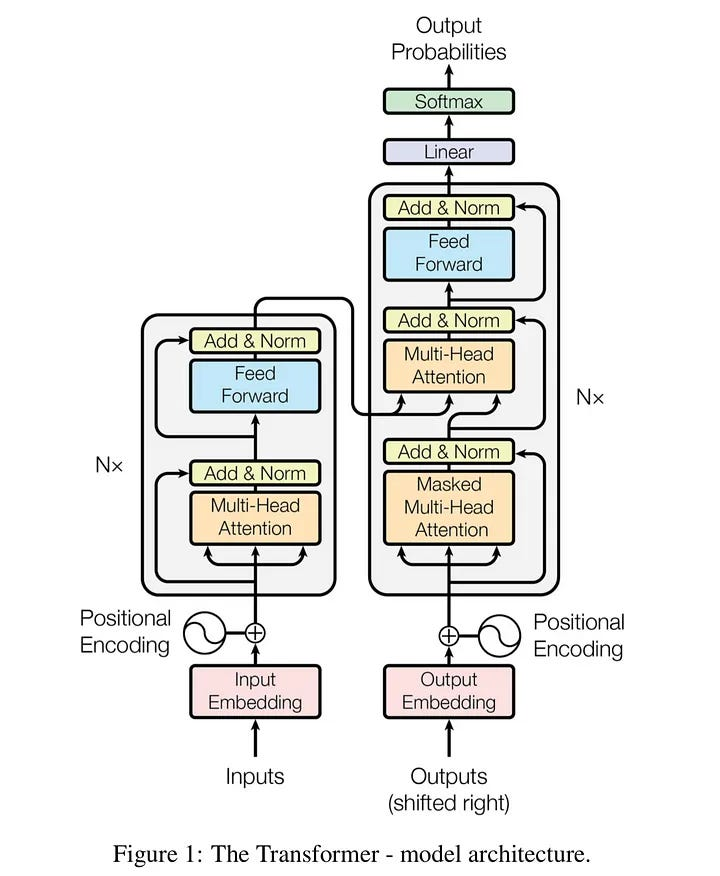
Architecture Detail

Self-Attention

自注意力机制允许模型在处理一个词时，权衡输入序列中其他所有词的重要性。它通过为序列中的每个词计算一个“注意力分数”来实现这一点，从而动态地决定关注哪些词。

图2: 一个自注意力头的可视化，展示了模型在编码"it"时如何将注意力分配给"The"和"animal"

self-attention的实现方式是Scaled Dot-Product Attention，核心是三个向量，$W^Q,W^K,W^V$; 这三个向量分别代表 Query - “我在寻找什么信息”，Key - “我能提供什么信息”，Value - “我包含的信息内容”；

单词向量（通过Embedding而来）$x$

Hint

打个比方： 你去图书馆找书（Query），书架上的标签就是 Key。当你发现某个标签和你的需求匹配时，你拿走的书中内容就是 Value。

具体计算过程，

1. 计算相似度: 将每个查询向量 Q 与所有键向量 K 进行点积，得到注意力分数。点积结果越高，说明这两个词越相关。

$$\text{Score}=Q\cdot K^T$$

2. 缩放（Scaling），将Score除以sqrt(d_k)（d_k是键向量的维度）以稳定梯度。

$$\text{Scaled Score}=\frac{Q\cdot K^T}{\sqrt{d_k}}$$

3. 归一化（Softmax），将Scpre转化为0-1的概率分布，代表每个单词对当前单词的“重要程度”；（Softmax后得到Attntion Weights，每一行都代表当前单词和剩下单词的关联程度的概率分布，每一行 sum = 1）
4. 加权求和（MatMul），将得到的权重乘以对应的 Value ($V$) 并求和。这样得到的向量就融合了全句的信息。

图3: Scaled Dot-Product Attention的计算流程图

即，

$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

Tip

Self-Attention有的优势在于，

• 捕捉长距离依赖： 无论两个词离多远，计算复杂度都是常数级别的
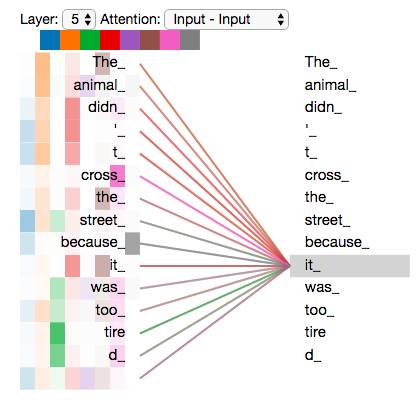
• 消除歧义： 比如在“The animal didn’t cross the street because it was too tired”中，自注意力会让 “it” 更多地关注 “animal”，而不是 “street”。
• 并行化： 不需要像 RNN 那样等待前一个词算完，所有词可以同时计算。

Self-Attention具体计算过程见：self_attention_example

Multi-Head Attention

单头注意力只能从一个“视角”来关注信息。为了让模型能从多个不同的角度理解数据（例如，同时关注语法结构、语义关系等），Transformer引入了多头注意力。

它通过在多个“子空间”中并行进行注意力计算来实现。每个头独立学习不同的注意力模式，然后将所有头的输出拼接起来，通过一个线性变换得到最终结果。

图4: 多头注意力机制示意图，输入被投影到多个头，并行计算注意力后拼接输出

具体例子见：multi_head_attention

Positional Encoding

Traditional Positional Encoding

Positional Encoding的传统做法（《Attention Is All You Need》原论文中）如下：

• 单词变向量： $X_{embed}=\text{Embedding}(X)$
• 生成位置向量： $P=\text{Positional Encoding}(pos)$
• 暴力相加： $Input=X_{embed}+P$

其中，位置向量不是通过简单的 $1,2,3,4$（数值会无限变大，破坏权重）,也不想用训练式的 Embedding（当时认为这无法处理比训练集更长的句子）。

对于第 $pos$ 个位置（比如第 5 个词），它的位置向量 $PE$ 的第 $i$ 个维度（偶数维度用 sin，奇数维度用 cos）的计算方式是：

$P{E}_{(pos,2i)}=\sin \left(\frac{pos}{10000^{2i/d_{model}}}\right)$ $P{E}_{(pos,2i+1)}=\cos \left(\frac{pos}{10000^{2i/d_{model}}}\right)$

• $pos$: 单词在句子中的位置（0, 1, 2…）。
• $i$: 向量维度的索引。
• $d_{model}$: 向量的总维度（比如 512）。

为了理解这个公式，别看数学，看物理逻辑。 想象一下我们要用数字表示位置：

• 十进制： 0, 1, 2, …, 9, 10 (个位变了，十位才变)。

• 二进制：

  • 000
  • 001 (最后一位变化最快)
  • 010 (中间位变化慢一点)
  • 011
  • 100 (第一位变化最慢)

Transformer 的这套公式，其实就是连续版本的二进制。

• 低维度（$i$ 很小）： 分母小，频率高。正弦波震荡得非常快。这就像时钟的秒针，稍微动一下位置，数值就变了。
• 高维度（$i$ 很大）： 分母大 ($10000^{...}$)，频率低。正弦波震荡得非常慢。这就像时钟的时针，走了很多步，数值才变一点点。

结论：

每一个位置 $pos$，都会生成一个独一无二的波纹指纹。模型看到这个指纹，就能反推出：“哦，你是第 5 个词”。

图5: 位置编码热力图

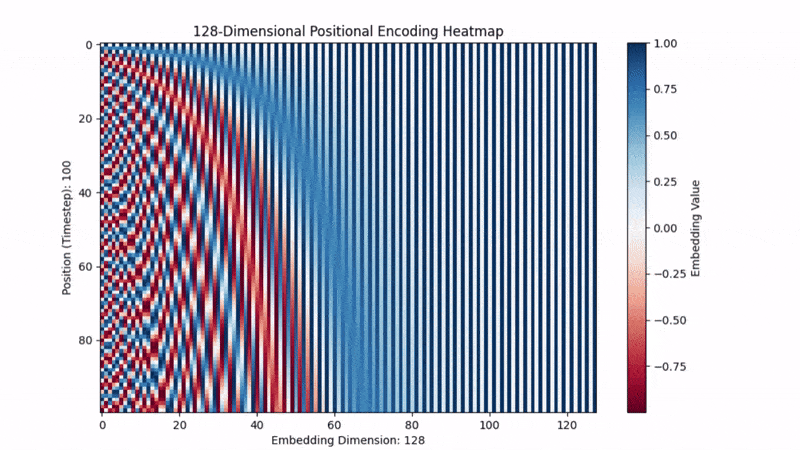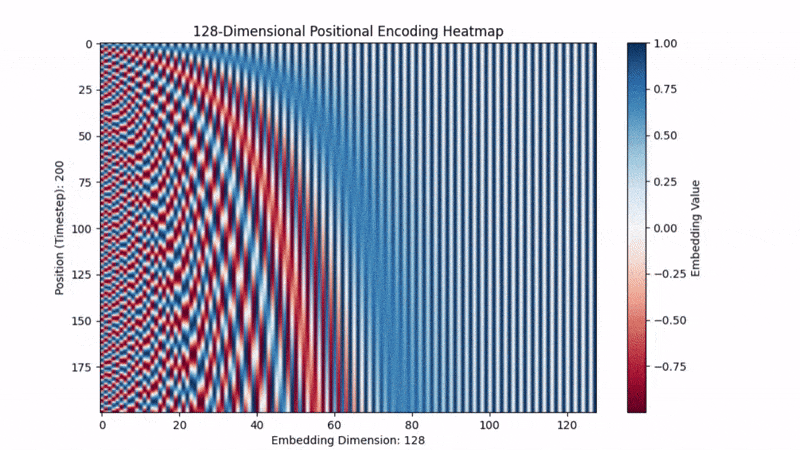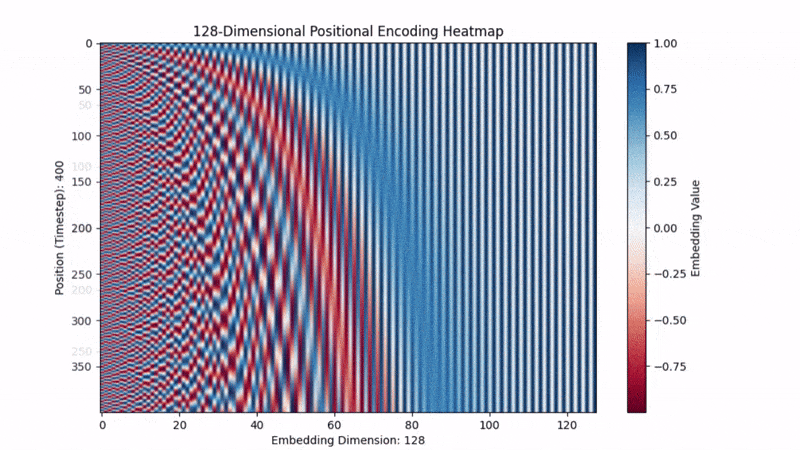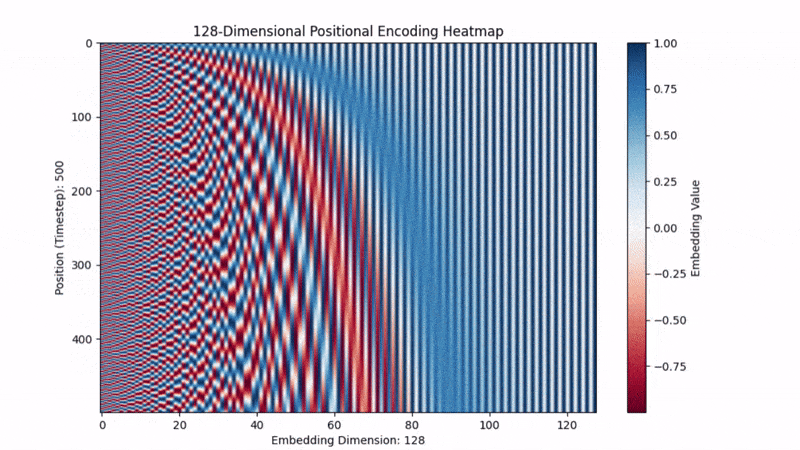
原作者选择正弦函数，不仅仅是因为它有周期性，更因为一个黄金数学性质：它可以让模型学会“相对位置”。 在三角函数公式中：

$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$ $\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

这意味着：

位置 $pos+k$ 的编码，可以表示为位置 $pos$ 的编码的线性变换（Linear Function）。

虽然我们给的是绝对位置（第1个，第2个…），但因为这个数学性质，模型在 Attention 做矩阵乘法时，理论上能够自动推导出来：“只要知道了我在 pos，我就能轻松算出 pos+k 的特征。 这就是为什么 Google 当时认为这套方案是完美的：既给了绝对位置，又隐含了相对位置信息。

第一反应可能是： “等等，Embedding 是语义信息（比如‘猫’），P 是位置信息（比如‘第1个’）。直接把这两个向量加起来，难道不会把‘猫’的含义搞乱吗？”

答案是：不会（或者说影响可控）。

• 高维空间的稀疏性： Transformer 的维度通常很大（比如 512 或 4096）。在这个高维空间里，语义信息和位置信息往往分布在不同的子空间里。虽然数值加在一起了，但模型在训练中能学会把它们“拆”开来看。

同时，Absolute Positional Encoding有个大问题是，“I walk my dog every day”和“every day I walk my dog”，这两个含义完全相同的句子，tokens却获得了全新的位置编码；因此 Relative Positional Encoding非常关键，可以帮助我们知道sequence order而无需担心它们的精确位置

PoRE(Rotary Positional Embedding)

PoRE的设的设计初衷是直接保证并利用相对位置信息，这是它相较于传统绝对位置编码（如Sinusoidal PE）的核心优势。

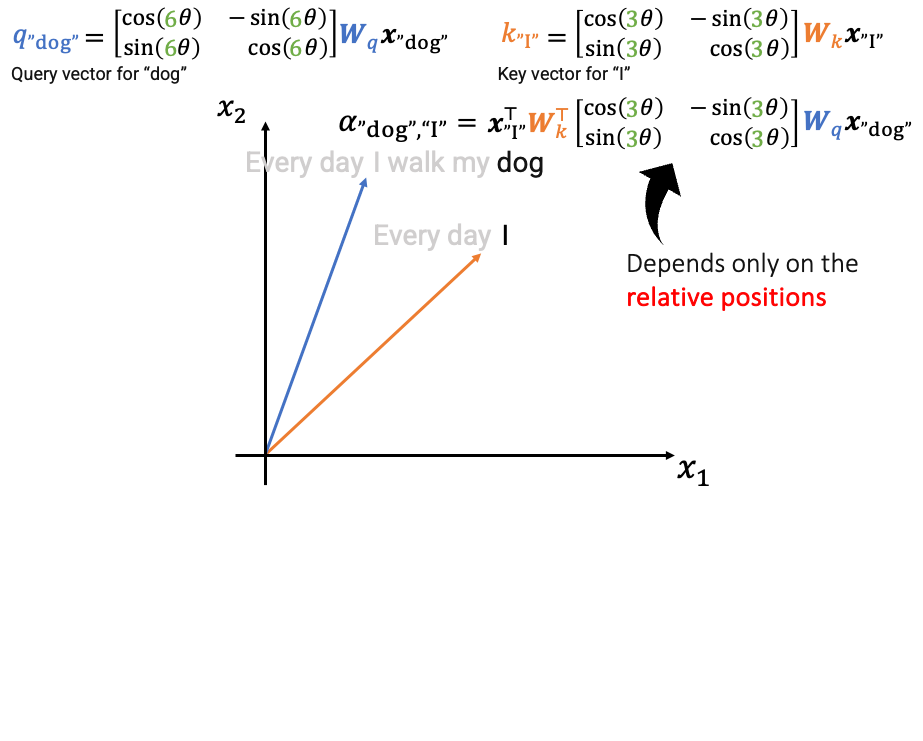
传统方法将位置信息“加”到词嵌入上，模型需要从绝对位置中“学习”相对关系。而PoRE的设计哲学是：让Attention分数（即$Q$和$K$的点积）本身就只依赖于词向量内容和它们之间的相对位置，从而在机制上先天保证相对位置的建模。

这可以用一个关键公式来说明。在应用PoRE后，处于位置$m$的词$Q_m$和处于位置$n$的词$K_n$，它们的点积计算结果是：

$$Q_m^T{K}_n=({\mathbf{R}}_{\theta ,m}{\mathbf{W}}_q{\mathbf{x}}_m{)}^T({\mathbf{R}}_{\theta ,n}{\mathbf{W}}_k{\mathbf{x}}_n)$$

其中，${\mathbf{R}}_{\theta ,m}$和${\mathbf{R}}_{\theta ,n}$是分别由位置$m$和$n$决定的旋转矩阵。这个设计的精妙之处在于，利用旋转矩阵的性质（${\mathbf{R}}_{\theta ,m}^T{\mathbf{R}}_{\theta ,n}={\mathbf{R}}_{\theta ,n-m}$），上面的公式可以简化为：

$$Q_m^T{K}_n=({\mathbf{W}}_q{\mathbf{x}}_m{)}^T{\mathbf{R}}_{\theta ,n-m}({\mathbf{W}}_k{\mathbf{x}}_n)$$

这个最终公式清晰地揭示了PoRE的设计初衷： 词$m$对词$n$的注意力分数$Q_m^T{K}_n$，仅仅依赖于原始的词向量投影$({\mathbf{W}}_q{\mathbf{x}}_m)$、$({\mathbf{W}}_k{\mathbf{x}}_n)$以及它们之间的相对位置差$(n-m)$。

总结一下：

• 初衷： 让自注意力机制能够直接、显式地建模相对位置关系，而不是依赖模型从绝对位置中推断。
• 实现方式： 通过对每一层的$Q$和$K$向量施加旋转变换（而非在输入层简单相加）。
• 核心公式体现： $Q_m^T{K}_n=({\mathbf{W}}_q{\mathbf{x}}_m{)}^T{\mathbf{R}}_{\theta ,n-m}({\mathbf{W}}_k{\mathbf{x}}_n)$。这个结果保证了注意力分数是词内容与相对位置$(n-m)$的函数，完美达成了设计目标。这使得模型在处理如“I walk my dog every day”和“every day I walk my dog”这样的句子时，能更好地理解词序变化下的语义一致性。

图6: PoRE

---

在实现detail上， PoRE不在输入层，而在每一层的 Attention 内部。

• 传统： Embedding + Position $\to$ 进入 Layer 1。
• RoPE： Embedding $\to$ 变成 $Q,K,V$ $\to$ 只对 $Q$ 和 $K$ 进行旋转 $\to$ 计算 $Q\cdot K^T$。

$x\stackrel{\text{Linear}}{\to }Q,K\stackrel{\text{RoPE (旋转)}}{\to }{Q}^{\prime },K^{\prime }\stackrel{\text{Dot Product}}{\to }\text{Attention Scores}$

RoPE 的核心思想是将向量看作复数平面上的点，通过旋转角度来注入位置信息。

• 分组： 把 $Q$ 和 $K$ 向量两两分组（比如 64 维分为 32 对）。

• 定义角度： 第 $m$ 个位置的 token，旋转角度为 $m\theta$。

• 旋转： 对每一对数值 $(x_1,x_2)$ 乘以一个旋转矩阵：

  $\left(\begin{array}{cc}\cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$ 例如， $Q=[1.0,0.0,1.0,0.0]$ RoPE 的第一步是 “切分” (Pairing)：它把这个 4 维向量，切成了 2 对 双胞胎。

• 第一对双胞胎 (Pair 1): 取前两个数 $[1.0,0.0]$。

  • 这里 $x_1=0.0$
  • 这里 $x_2=1.0$

• 第二对双胞胎 (Pair 2): 取后两个数 $[1.0,0.0]$。

  • 这里 $x_1=1.0$
  • 这里 $x_2=0.0$

这就是 $(x_1,x_2)$ 的真面目：它们就是向量里原本就有的数字，只是被我们两个两个地拎出来处理了。

第二步，计算“转速” $\theta$（这是变慢的关键！）。RoPE 规定，每一对的旋转基础角度 ${\theta }_i$ 是通过固定公式算出来的：

${\theta }_i=\frac{1}{10000^{2i/d}}$

• $d=4$ (总维度)
• $i$ = 当前是第几对

1. 第 0 对 ($i=0$) 的转速：

${\theta }_0=\frac{1}{10000^{2\times 0/4}}=\frac{1}{10000^0}=\frac{1}{1}=1$

结论： 第 0 对的基础转速是 1 弧度/步（约 57 度）。非常快！

2. 第 1 对 ($i=1$) 的转速：

${\theta }_1=\frac{1}{10000^{2\times 1/4}}=\frac{1}{10000^{0.5}}=\frac{1}{\sqrt{10000}}=\frac{1}{100}=0.01$

结论： 第 1 对的基础转速是 0.01 弧度/步（约 0.57 度）。超级慢！

第一对每次转 57 度，像风扇一样狂转。 第二对每次只转 0.5 度，像乌龟一样挪动。这就是“频率衰减”。

现在从第一个单词开始，所以 $m=1$。 我们需要旋转的总角度是：$\text{总角度}=m\times \theta$。

处理第 0 对：高速组 $[1.0,0.0]$

• 旋转角度： $1\times 1=1$ 弧度。

• 计算：

  $\left(\begin{array}{c}{x}_0^{\prime }\\ x_1^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos (1)& -\sin (1)\\ \sin (1)& \cos (1)\end{array}\right)\left(\begin{array}{c}1.0\\ 0.0\end{array}\right)$

  (查表得：$\cos (1)\approx 0.54,\sin (1)\approx 0.84$)

  $x_0^{\prime }=1.0\times 0.54-0.0\times 0.84=0.54$

  $x_1^{\prime }=1.0\times 0.84+0.0\times 0.54=0.84$

  结果： 向量从 $[1,0]$ 变成了 $[0.54,0.84]$。变化非常大！

处理第 1 对：低速组 $[1.0,0.0]$

• 旋转角度： $1\times 0.01=0.01$ 弧度。

• 计算： $\left(\begin{array}{c}{x}_2^{\prime }\\ x_3^{\prime }\end{array}\right)=\left(\begin{array}{cc}\cos (0.01)& -\sin (0.01)\\ \sin (0.01)& \cos (0.01)\end{array}\right)\left(\begin{array}{c}1.0\\ 0.0\end{array}\right)$

  (近似：$\cos (0.01)\approx 1.0,\sin (0.01)\approx 0.01$)

  $x_2^{\prime }=1.0\times 1.0-0.0\times 0.01\approx 1.0$ $x_3^{\prime }=1.0\times 0.01+0.0\times 1.0\approx 0.01$ 结果： 向量从 $[1,0]$ 变成了 $[1.0,0.01]$。几乎没动！

我们把最终结果拼起来看：

• 原始向量： [1.0, 0.0, 1.0, 0.0]
• RoPE后向量： [0.54, 0.84, 1.0, 0.01]

这说明了什么？

1. 前两维（快针）：它是“秒针”。 如果单词从位置 1 挪到位置 2，这两维的数值会剧烈跳变（比如转到负数去）。它们负责告诉模型：“我是第 1 个词，不是第 2 个词”。（区分近距离）
2. 后两维（慢针）：它是“时针”。 单词从位置 1 挪到位置 2，它几乎不动。只有当单词挪到第 100 个位置时，它才会转过明显的角度。它们负责告诉模型：“我在句子的前半段，不在后半段”。（区分长距离）

解决周期性问题：如果所有维度都像“秒针”一样高速旋转，那么位置$m$和位置$m+360$的编码在经过360度旋转后会变得完全相同，模型将无法区分它们。低速维的存在避免了这一点，因为它们在长距离内才会累积出显著变化，从而为超长序列中的每个位置生成一个几乎唯一的复合编码“指纹”。

实现多尺度感知：模型可以同时利用不同频率的维度。当判断两个词是否相邻时，它更依赖高速维的显著差异；当判断两个词是否属于同一个长段落或章节时，它则参考低速维的相似性。

---

同时，RoPE技术还跟Training Context Length有很大的关系，这部分我们详细见：RoPE_detail

Transformer Arch

Encoder-Decoder

2017 年《Attention is All You Need》论文中的原始形态，最初是为机器翻译设计的。

• *Encoder（编码器）： 负责“理解”。它通过多层 Self-Attention 查看整个输入句子，把每个词转化成包含上下文信息的向量。
• Decoder（解码器）： 负责“生成”。它比 Encoder 多了一个 Cross-Attention（交叉注意力） 层。
  • Cross-Attention： Decoder 会拿着自己已经生成的词，去询问 Encoder：“原文里哪些信息对我生成下一个词最重要？”

• 输入端： Input $\to$ Embedding + Positional Embedding $\to$ Encoder。
• 中间桥梁： Encoder 输出的“特征矩阵”被送往 Decoder 的每一层。
• 输出端： Decoder 结合已生成的词和 Encoder 的信息，逐个预测下一个词。

Encoder-only & Decoder-only

随着研究深入，人们发现这两个模块其实可以拆开单独使用，这也开启了 NLP 的两个大时代。

Encoder-only (代表作：BERT)

• 结构： 只保留左半边。
• 特点： “全向看”。计算某个词时，它能看到句子中左边和右边所有的词。
• 擅长： 文本分类、命名实体识别、阅读理解。因为它能透彻地理解上下文，但由于它“预知了未来（看到了右边的词）”，所以很难用来做流畅的文本生成。

Decoder-only (代表作：GPT 系列)

• 结构： 只保留右半边，但去掉了 Cross-Attention（因为没有 Encoder 了）。
• 特点： “向左看”。由于使用了 Masked Self-Attention（掩码自注意力），它在生成第 $n$ 个词时，只能看到前 $n-1$ 个词。
• 擅长： 预测下一个词。

LLM：Decoder-only？

从 BERT（Encoder-only）统治世界到 GPT（Decoder-only）一统江湖，主要有以下几个深层原因：

A. 训练效率与规模化（Scalability）

Encoder-Decoder 结构虽然强大，但参数量分布在两个模块中。研究发现，将所有参数集中在一个统一的 Decoder 架构下，模型在海量数据上的学习效率更高。随着参数规模达到千亿级，Decoder-only 展现出了更强的涌现能力（Emergent Abilities）。

B. 任务的统一性

LLM 的本质是“文本续写”。

• Encoder-only 适合判别任务，但生成能力弱。
• Encoder-Decoder 适合翻译，但在处理复杂的开放式对话、逻辑推理时，Encoder 的预处理有时反而限制了模型生成的自由度。
• Decoder-only 把一切任务（翻译、分类、代码、创作）都转化成了“预测下一个词”。这种极简的逻辑在工程实现上极其稳定。

C. 零样本推理（Zero-shot Learning）

Decoder-only 架构在预训练阶段就是在做“根据上文填空”。这让它天然适应 Prompt（提示词）模式。你给它一段指令，它会自然而然地沿着指令往下补全，这种特性是 BERT 等模型很难模拟的。

Interview-Question

为什么 Scaling 要除以 $\sqrt{d_k}$？

为了“防止梯度消失”，稳定梯度。

主要原因是因为Softmax的函数特性，如果不除以 $\sqrt{d_k}$，会造成点积爆炸；假设 $Q$ and $K$ 的维度 ($d_k$) 很大，比如 512。 当我们在做点积 ($Q\cdot K^T$) 时，是在将 512 个数字相乘再相加，会导致数值范围变得非常大。

Softmax函数公式是$\frac{e^x}{\sum e^x}$，对输入的数值大小非常敏感；例如[20,30]，$e^{20}\approx 4.8\times 10^8$ $e^{30}\approx 1.0\times 10^{13}$ ，权重：$\approx [0.00004,0.99996]$；

Softmax 的分布变得像“独热编码 (One-hot)”一样极端。其中一个不仅拿走了所有权重，而且在数学上，Softmax 函数在趋近于 0 或 1 的位置，导数（梯度）趋近于 0。

以至于为什么要除以$\sqrt{d_k}$，假设 $Q$ 和 $K$ 中的每个元素都是均值为 0，方差为 1 的随机变量。它们的点积 $Q\cdot K={\sum }_{i=1}^{d_k}{q}_i{k}_i$。[根据统计学规律，如果你把 $d_k$ 个方差为 1 的数加起来，结果的方差会变成 $d_k$]((math/statistic/basic_concepot/var_addition.md)。这意味着点积结果的标准差变成了 $\sqrt{d_k}$，因此需要把结果除以标准差，让数值保持在 Softmax 喜欢的“舒适区”。

为什么要使用softmax归一化weight matrix？

但 Softmax 最终成为了 Transformer 的标准配置，主要原因不是因为它“好算”，而是因为它具备一个简单的归一化（Sum）无法提供的核心特性：“赢家通吃” (Winner-Take-All) 的倾向性，同时又保持了可导性。

1.核心差异：放大信号，抑制噪声

注意力机制的本质是**“查字典”。当我在找东西时，我希望找到那个最匹配的，而忽略掉那些一般般**的。

假设我们算出来的 Score 是：[10, 9, 2]。

• 10 是最相关的（目标）。
• 9 是干扰项（只差一点点）。
• 2 是完全不相关的背景噪声。

方案 A：直接按和分配 (Linear Normalization)

我们把它们加起来：$10+9+2=21$。

然后算权重：

• $w_1=10/21\approx 0.48$
• $w_2=9/21\approx 0.43$
• $w_3=2/21\approx 0.10$

结果： 0.48 和 0.43 几乎没有区别！模型会变得**“犹豫不决”**。它混入了大量干扰项（9）的信息，导致最终提取出的特征变得模糊。

方案 B：Softmax

我们计算 $e^x$：

• $e^{10}\approx 22026$
• $e^9\approx 8103$
• $e^2\approx 7$
• 总和 $\approx 30136$

权重：

• $w_1\approx 0.73$
• $w_2\approx 0.27$
• $w_3\approx 0.0002$

结果：

1. 拉开差距： 原始分数只差 1 (10 vs 9)，经过 Softmax 后，权重差距变成了近 3 倍 (0.73 vs 0.27)。Softmax 敏锐地放大了“稍微好一点”的那个选项。
2. 降噪： 那个得分为 2 的噪声，被彻底压到了 0。

结论： Softmax 是一种 “软性的最大值” (Soft Maximum)。它让模型能够聚焦 (Focus)。如果用简单的 Sum，模型就变成了“雨露均沾”，失去了注意力的意义。

---

2. 数学上的必须性：非负性 (Positivity)

“直接根据 Sum 来分配 weight”，公式大概是 $w_i=\frac{Scor{e}_i}{\sum Score}$。这里有一个巨大的隐患：点积算出来的 Score 可以是负数！

• 如果 $Q=[1,-1]$，$K=[-1,1]$，点积是 $-2$。
• 如果你的 Score 列表是 [10, -5, -8]。
• 求和是 $-3$。
• 第一项的权重变成 $10/-3=-3.33$。

权重变成了负数？ 这在注意力机制里解释不通。我们要的是“加权平均”，通常要求权重必须是正的且和为 1（凸组合），这样才能保证输出的向量 $V$ 不会飞出原本的特征空间。

Softmax 的优势：

$e^x$ 永远是正数。不管你的点积算出 $-100$ 还是 $-10000$，Softmax 都能把它变成一个正的概率值（虽然很小），保证了加权求和在数学上的稳定性。

---

3. 梯度的“选拔”作用

你说 Softmax 导致梯度需要缩放（防止梯度消失），这是它的缺点。但反过来看，Softmax 的梯度特性正是它能训练出好模型的关键。

Softmax 的导数特点是：只有当两个分数的竞争非常激烈时，梯度才最大。

• 如果一个是 100，一个是 0（胜负已分），Softmax 认为不需要调整了，梯度趋近 0。
• 如果一个是 10，一个是 9.9（难分伯仲），Softmax 会产生很大的梯度，告诉前面的层：“嘿，你得把这两个区分开！去更新权重，让 10 变得更大，让 9.9 变得更小！”

这种机制迫使模型去学习如何区分相似的词，而不是仅仅记住一堆平均值。

---

4. 总结

为什么一定要 Softmax，哪怕要为了它专门搞一个 Scaling？

1. 非线性 (Non-linearity)： 神经网络需要非线性才能拟合复杂函数。单纯的除以 Sum 是线性变换，能力有限。
2. 聚焦 (Selectivity)： Softmax 能把微小的分数差异放大，让模型敢于“做决定”，关注最重要的那个词。
3. 非负性 (Positivity)： $e^x$ 解决了点积出现负数时权重分配的数学灾难。
4. 可导的 Hardmax： 我们其实最想要的是 Hardmax（只取最大的那个，其他全为0），但 Hardmax 不可导。Softmax 是我们能找到的、最接近 Hardmax 且处处可导的完美替代品。

所以，Scaling ($÷\sqrt{d_k}$) 就像是我们要使用 Softmax 这把“利剑”所必须支付的“保养费”。为了它的聚焦能力，这个代价是值得的。

什么是LayerNorm，什么是BatchNorm，为什么Transformer选择LayerNorm的做法，而CNN选择BatchNorm？

1. 什么是 BatchNorm (批归一化)？

BatchNorm 是在批次维度 (Batch Dimension) 上进行归一化。对于一个批次 (Batch) 的数据：

• 操作对象：对 同一个特征通道，计算该批次内所有样本的均值和方差，然后用这个统计量来归一化该通道的所有值。
• 直观理解：假设你的批次有 N 个句子，每个句子的词向量是 D 维。BatchNorm 会独立处理这 D 维中的每一维（比如第1维，代表“名词性”）。它会收集这 N 个句子中所有词的第1维数值，算出均值和方差，然后对这 N 个句子的所有词的第1维进行归一化。
• 公式（对于某个特征维度）： $\text{BN}(x)=\gamma \cdot \frac{x-{\mu }_{\text{Batch}}}{\sqrt{{\sigma }_{\text{Batch}}^2+ϵ}}+\beta$ 其中 ${\mu }_{\text{Batch}}$ 和 ${\sigma }_{\text{Batch}}^2$ 是当前批次在该维度上的均值和方差。
• 优点：
  • 减少内部协变量偏移：使每一层的输入分布更稳定，加速训练。
  • 有一定的正则化效果：因为使用批次统计量，引入了噪声。
• 缺点：
  • 依赖批次大小：在小批次（Batch Size）下统计量不准确，影响性能。
  • 不适合动态序列：在 RNN 或 Transformer 中，序列长度可能变化，不同位置（时间步）的统计量可能不同，用同一个批次统计量归一化所有位置不合理。

2. 什么是 LayerNorm (层归一化)？

LayerNorm 是在特征维度 (Feature Dimension) 上进行归一化。对于单个样本（例如一个词向量或一个序列）：

• 操作对象：对 单个样本，计算其所有特征维度的均值和方差，然后用这个统计量来归一化该样本的所有特征值。
• 直观理解：对于序列中的一个词向量（D 维），LayerNorm 会计算这个词向量本身 D 个数值的均值和方差，然后用它们来归一化这个词向量。它不关心批次中其他样本的情况。
• 公式（对于单个样本/词向量）： $\text{LN}(x)=\gamma \cdot \frac{x-{\mu }_{\text{Layer}}}{\sqrt{{\sigma }_{\text{Layer}}^2+ϵ}}+\beta$ 其中 ${\mu }_{\text{Layer}}$ 和 ${\sigma }_{\text{Layer}}^2$ 是该样本所有特征维度的均值和方差。
• 优点：
  • 不依赖批次大小：统计量在单个样本上计算，因此训练和推理时行为一致，不受批次大小影响。
  • 适合序列模型：对变长序列友好，每个时间步（词）独立归一化。

3. 为什么Transformer选择LayerNorm的做法，而CNN选择BatchNorm

CNN选择BatchNorm，Transformer选择LayerNorm，是由它们各自处理的“数据特性”和“架构需求”共同决定的。

下图直观地展示了这一核心差异：

flowchart TD
    A[输入数据] --> B{数据维度与结构}
    
    B --> C[图像数据<br>（CNN处理）]
    B --> D[序列数据<br>（Transformer处理）]
    
    C --> E[特点：固定网格结构<br>同一特征图在不同位置分布相似]
    D --> F[特点：可变长度序列<br>不同位置统计特性差异大]
    
    E --> G[核心需求：跨样本统一特征分布<br>（让不同图片的“边缘”特征可比）]
    F --> H[核心需求：样本内特征稳定<br>（让每个词向量的不同维度可比）]
    
    G --> I[选择：BatchNorm<br>沿批次维度归一化]
    H --> J[选择：LayerNorm<br>沿特征维度归一化]
    
    I --> K[完美契合CNN<br>稳定训练，提供正则化]
    J --> L[完美契合Transformer<br>长度无关，稳定注意力机制]

下面我们来详细拆解这背后的原因：

核心差异：处理的数据结构不同

维度	CNN（图像）	Transformer（序列）
数据形状	[Batch, Channels, Height, Width]	[Batch, Sequence_Length, Feature_Dim]
核心特性	空间不变性 (Spatial Invariance)	序列可变性 (Variable Length)
任务焦点	识别特征（如边缘、纹理），这些特征在不同图片、不同位置应具有一致的统计分布。	理解关系（词与词、token与token之间的关系），每个位置的上下文都独一无二。

为什么CNN钟爱BatchNorm？

1. 数据特性匹配：对于一张图片，CNN的每个通道（例如，一个检测“垂直边缘”的滤波器）的输出，在整张图片的不同位置（如左上角和右下角）理论上应该服从相似的分布。BatchNorm沿批次维度对每个特征通道进行归一化，正是利用了这一点：它假设“批次中所有图片的‘垂直边缘’特征图，其分布是相似的”。这种跨样本的归一化能有效加速训练。
2. 输入尺寸固定：图像任务通常将图片缩放到固定尺寸（如224x224），因此Height和Width维度是确定的。这使得跨批次计算同一空间位置（尽管不常见）或同一通道的统计量变得可行且稳定。
3. 正则化效应：BatchNorm在训练时使用当前批次的统计量，在推理时使用移动平均的统计量。这种不一致性无意中引入了一种噪声，起到了轻微的正则化效果，有助于防止过拟合，这在图像分类任务中非常有益。
4. 稳定卷积输出：卷积层的输出值范围会受到权重初始化和输入数据的很大影响。BatchNorm通过强制每个通道的激活值具有零均值和单位方差，为后续层提供了稳定、标准化的输入，极大缓解了梯度问题。

简单比喻：CNN像是一个工厂的质检员，用同一套标准（BatchNorm统计量）去检查不同产品（批次中的不同图片）的同一个零件（特征通道）是否符合规格。

为什么Transformer依赖LayerNorm？

1. 处理可变长序列：这是最根本的原因。文本序列长度千差万别。如果使用BatchNorm，就需要对批次中所有序列的第1个位置、第2个位置…… 分别计算均值和方差。但短序列的尾部是填充符(Padding)，长序列的中间位置语义复杂，这些位置的统计量混合在一起毫无意义，会严重破坏模型性能。
2. 样本独立计算：LayerNorm对每个序列、每个词向量（Token） 独立进行归一化。它计算的是一个词向量所有维度（如512维）的均值和方差。这完美避开了序列长度和批次大小的影响，使得训练和推理过程完全一致，非常稳定。
3. 与自注意力机制协同：自注意力机制的核心是计算 $Q{K}^T$ 点积和 Softmax。这些操作对输入向量的幅度（Scale） 非常敏感。LayerNorm确保输入到自注意力层的每个词向量都被归一化到相似的尺度，为注意力权重的动态计算提供了一个稳定的起点，防止梯度爆炸或消失。
4. 适合自回归生成：在推理时，Transformer（尤其是Decoder）通常是逐个Token生成的（批次大小可能为1）。BatchNorm在单样本下的统计量毫无意义，而LayerNorm在任何情况下都能正常工作。

简单比喻：Transformer像是一位同声传译，它必须独立地、即时地处理每一句 incoming speech（每个序列），并专注于理清这句话内部各个词语（每个词向量的各个维度）之间的关系，而无暇顾及之前其他句子的情况。

总结对比表

考量因素	CNN (使用 BatchNorm)	Transformer (使用 LayerNorm)
数据假设	同一特征在不同样本、不同位置分布相似	每个序列、每个位置的上下文都独特
长度处理	输入尺寸固定，无需处理变长	必须优雅地处理可变长序列
批次依赖	依赖足够大的批次以获得准确统计量	完全独立于批次大小，小批次或单样本均可
与架构协同	稳定卷积层输出，配合其空间不变性	稳定自注意力计算，匹配其动态权重特性
推理一致性	训练/推理统计量不同，需用移动平均	训练/推理行为完全一致

结论：BatchNorm和LayerNorm的“分工”是深度学习中的一个经典范例。它告诉我们，没有“最好”的技术，只有“最合适”的技术。CNN因其处理具有空间不变性的网格数据的特性而与BatchNorm联姻；Transformer因其处理长度可变、关系复杂的序列数据的使命而与LayerNorm结盟。这种选择是数据特性、计算需求和架构设计三者完美契合的结果。

Reference

• Understanding Transformer Sinusoidal Position Embedding
• Understanding Positional Encoding in Transformers
• How Rotary Position Embedding Supercharges Modern LLMs
• RoPE PPT Slides