Dynamic Time Warping (DTW)

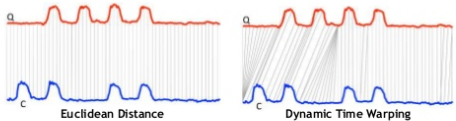
欧氏距离在时间序列之间可能是一个不好的选择，因为时间轴上存在扭曲的情况。DTW 是一个考虑到这种扭曲的，测量距离来比较两个时间序列的一个指标，本section讲解如何计算 DTW distance

Detail

Step 1. 准备输入序列

假设两个time series, A & B

Step 2. 计算距离矩阵

创建一个距离矩阵，其中的元素表示序列 A 和序列 B 中每个时间点之间的距离。常见的距离度量方法包括欧氏距离、曼哈顿距离、余弦相似度等。根据你的数据类型和需求选择适当的距离度量方法。

Step 3. 初始化累积距离矩阵

创建一个与距离矩阵大小相同的累积距离矩阵，用于存储从起点到每个位置的累积距离。将起点 (0, 0) 的累积距离设为距离矩阵的起始点距离。

Step 4. 计算累积距离

从起点开始，按照动态规划的方式计算累积距离矩阵中每个位置的累积距离。对于每个位置 (i, j)，累积距离等于该位置的距离加上三个相邻位置中选择最小累积距离的值。

$$DTW(i,j)=d_{i,j}+\min \{DTW(i-1,j),DTW(i,j-1),DTW(i-1,j-1)\}$$

Step 5. 回溯最优路径

从累积距离矩阵的最右下角开始，根据最小累积距离的路径回溯到起点 (0, 0)。记录下经过的路径，即为最优路径。

Step 6. 计算最终距离

根据最优路径上的累积距离，计算出最终的 DTW 距离。

Example

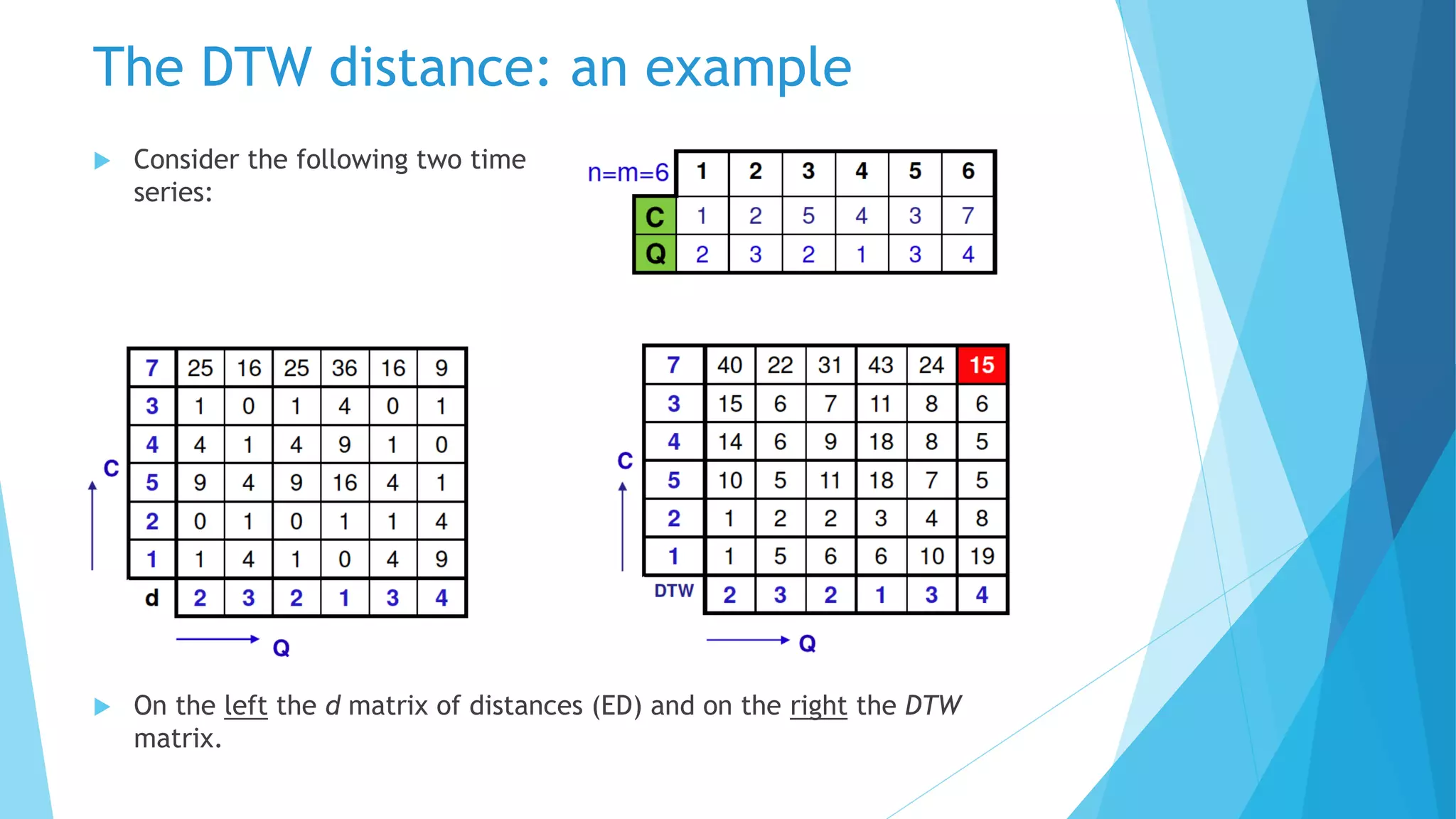
左边是距离矩阵，右边是DTW矩阵，也就是累积距离矩阵

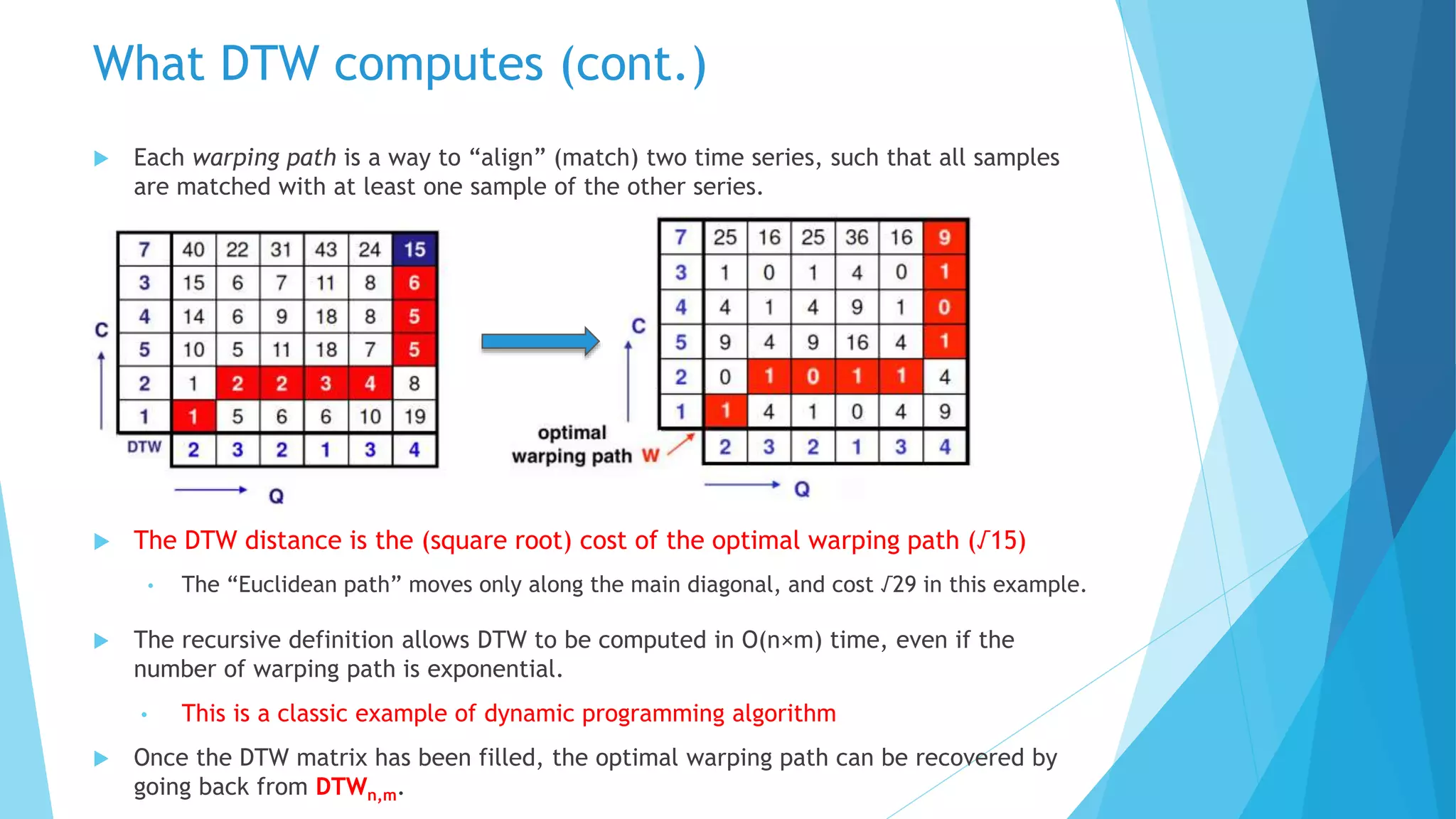
通过回溯，找到optimal warping path，DTW distance就是 the optimal warping path的square root，本例中就是$\sqrt{15}$