SHAP - a reliable way to analyze model interpretability

SHAP is the most popular model-agnostic technique that is used to explain predictions. SHAP stands for SHapley Additive exPlanations

Shapely values are obtained by incorporating concepts from Cooperative Game Theory  and local explanations

Mathematical and Algorithm Foundation

Shapely Values

Shapely values were from game theory and invented by Lloyd Shapley. Shapely values were invented to be a way of providing a fair solution to the following question:

Question

If we have a coalition C that collaborates to produce a value V: How much did each individual member contribute to the final value

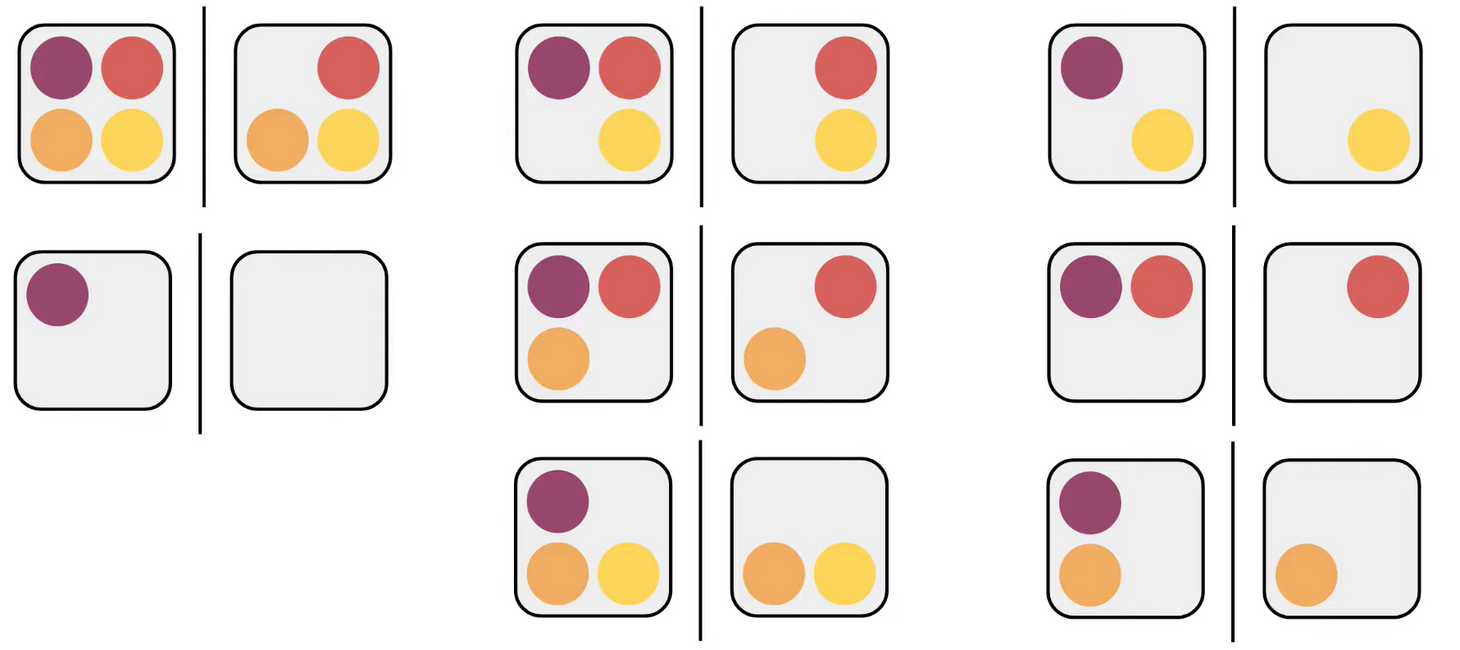
The method here we assess each individual member’s contribution is to removing each member to get a new coalition and then compare their production, like this graphs:

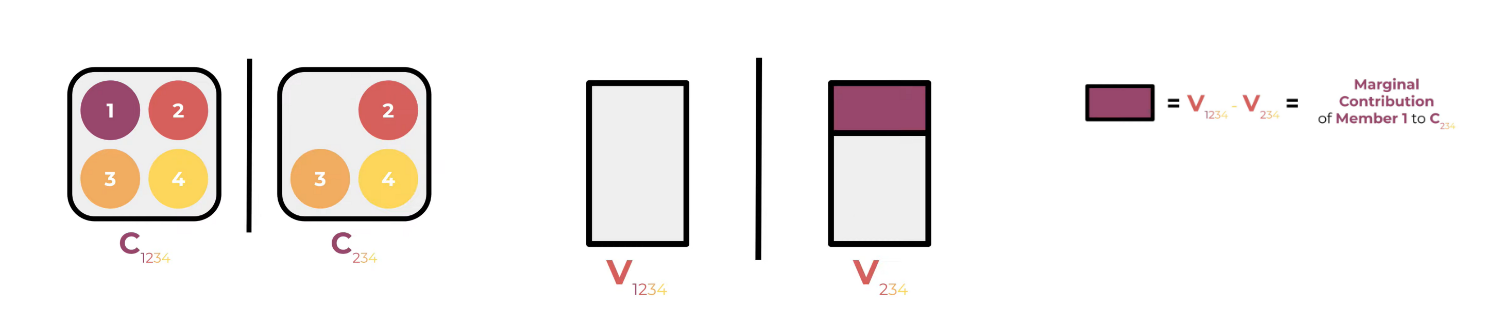
And then, we get every member 1 included or not included coalitions like this:

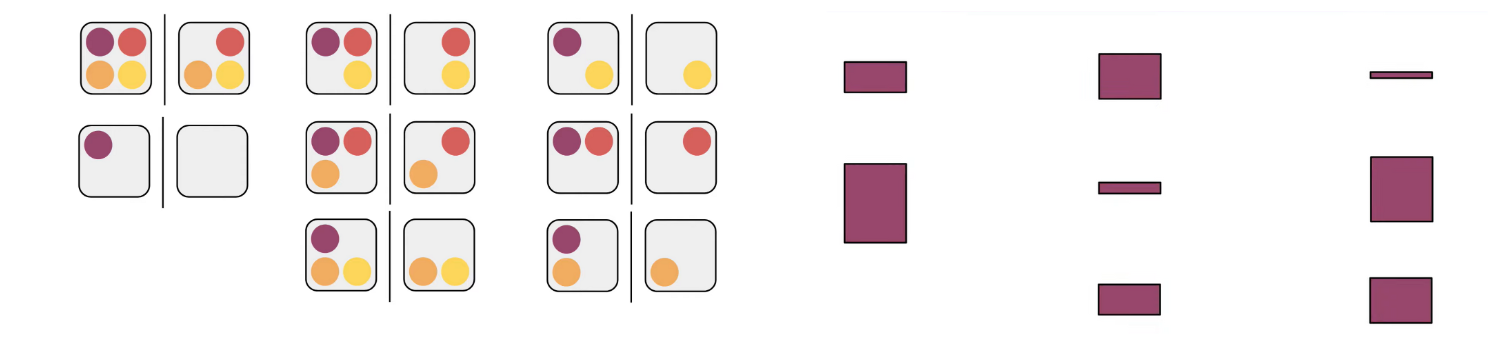
Using left value - right value, we can get difference like image left above; And then we calculate the mean of them:

$${\phi }_i=\frac{1}{\text{Members}}\sum _{\forall \text{C s.t. i}\notin \text{C}}\frac{\text{Marginal Contribution of i to C}}{\text{Coalitions of size |C|}}$$

Shapely Additive Explanations

We need to know what’s additive mean here. Lundberg and Lee define an additive feature attribution as follows:

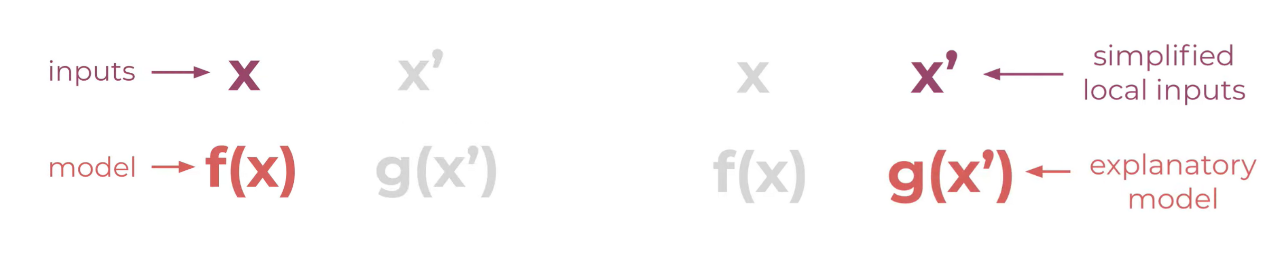
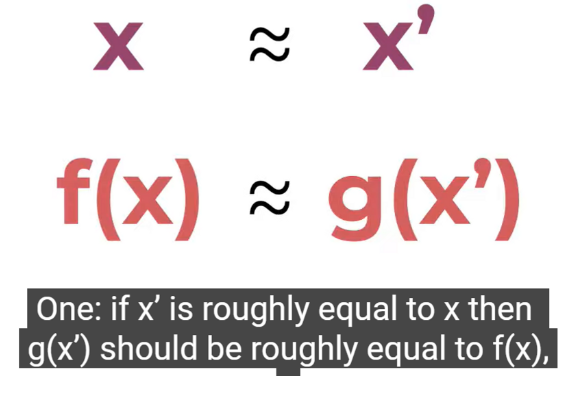
$x^{\prime }$, the simplified local inputs usually means that we turn a feature vector into a discrete binary vector, where features are either included or excluded. Also, the $g(x^{\prime })$ should take this form:

$$g(x^{\prime })={\phi }_0+\sum _{i=1}^N{\phi }_i{x^{\prime }}_i$$

• ${\phi }_0$ is the null output of this model, that is, the average output of this model

• ${\phi }_i$ is feature affect, is how much that feature changes the output of the model, introduced above. It’s called attribution

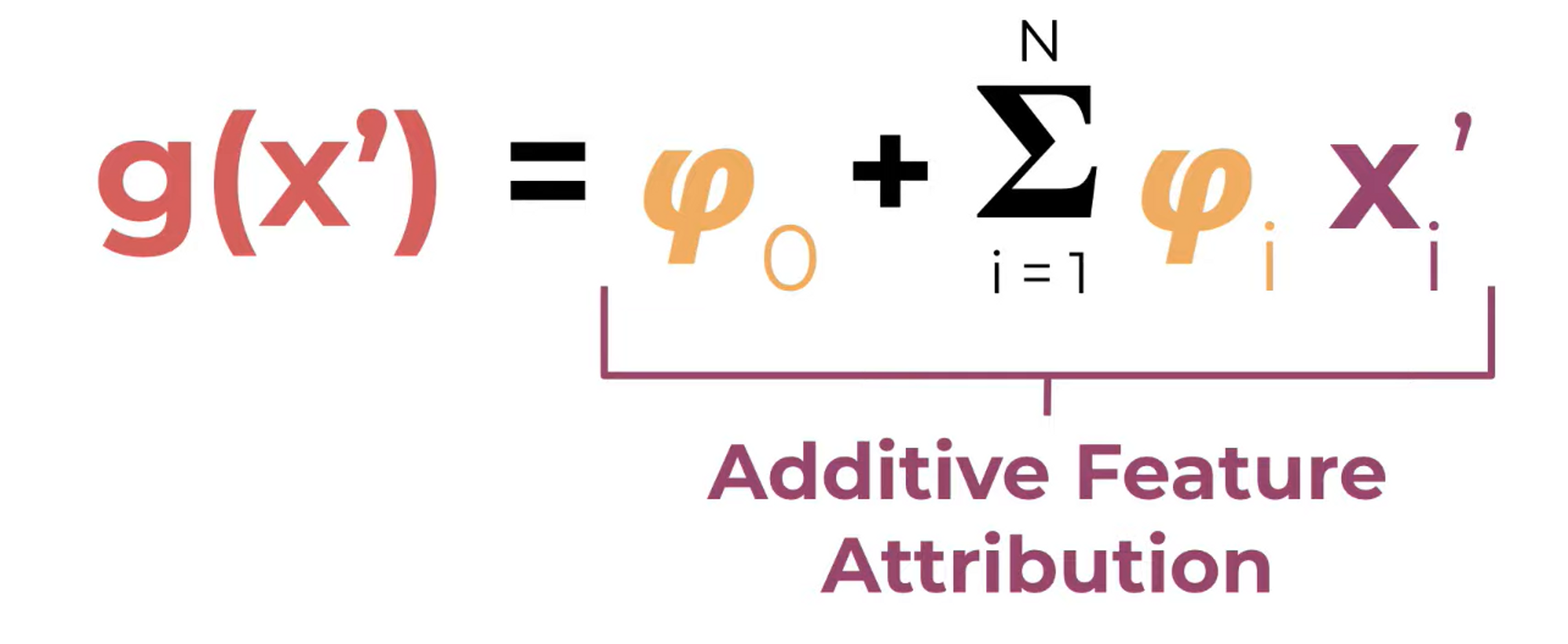
Now Lundberg and Lee go on to describe a set of three desirable properties of such an additive feature method, local accuracy, missingness, and consistency.

Local accuracy

$$g(x^{\prime })\approx f(x)\text{if}{x}^{\prime }\approx x$$

Missingness

$${x_i}^{\prime }=0\to {\phi }_i=0$$

if a feature excluded from the model. it’s attribution must be zero; that is, the only thing that can affect the output of the explanation model is the inclusion of features, not the exclusion.

Consistency

If feature contribution changes, the feature effect cannot change in the opposite direction

Why SHAP

Lee and Lundberg in their paper argue that only SHAP satisfies all three properties if the feature attributions in only additive explanatory model are specifically chosen to be the shapley values of those features

SHAP, step-by-step Process, same as shap.explainer

For example, we consider a ice cream shop in the airport, it has four features we can know to predict his business.

$$\begin{gathered} \left[\begin{array}{cccc}\text{temperature}& \text{day of weeks}& \text{num of flights}& \text{num of hours}\end{array}\right] \\ \to \\ \left[\begin{array}{cccc}T& D& F& H\end{array}\right] \end{gathered}$$

For, example, we want to know the temperature 80 in sample [80 1 100 4] shapley value, here’s the step

• Step 1. Get random permutation of features, and give a bracket to the feature we care and everything in its right. (manually)

$$\left[\begin{array}{ccc}F& D& \underbrace{TH}\end{array}\right]$$

• Step 2. Pick random sample from dataset

For example, [200 5 70 8], form: [F D T H]

• Step 3. Form vectors $x_1{x}_2$

$$x_1=[1001808]$$

$x_1$ is partially from original sample and partially from the random chosen one, the feature in bracket will from random chosen one, exclude what we care

$$x_2=[1001708]$$

$x_2$ just change the feature we care into the same as random chosen one’s feature value

Then, calculate the diff and record

$$DIFF=c_1-c_2$$

• Step 4. Record the diff & return to step 1. and repeat many times

$$\text{SHAP}(T=80|[8011004])=\text{average(DIFF)}$$

Shapley kernel

Too many coalitions need to be sampled

Like we introduce shapley values above, for each ${\phi }_i$ we need to sample a lot of coalitions to compute the difference.

For 4 features, we need 64 total coalitions to sample; For 32 features, we need 17.1 billion coalitions to sample.

It’s entirely untenable.

So, to get over this difficulty, we need devise a shapley kernel, and that’s how the Lee and Lundberg do

Detail

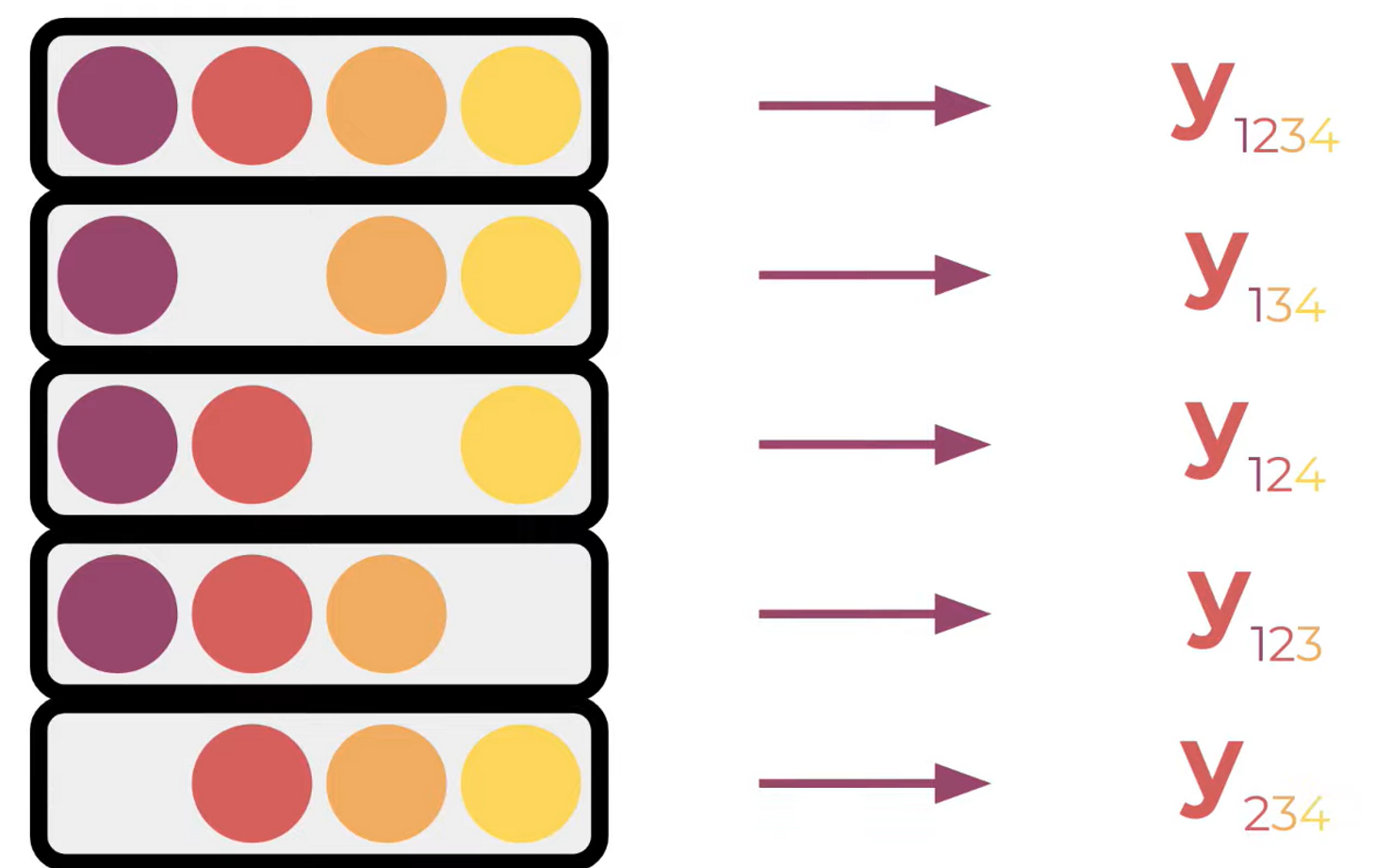
Though most of ML models won’t just let you omit a feature, what we do is define a background dataset B, one that contains a set of representative data points that model was trained over. We then filled in out omitted feature of features with values from background dataset, while holding the features are included in the permutation fixed to their original values. We then take the average of the model output over all of these new synthetic data point as our model output for that feature permutation which we call $\bar{y}$.

$$E[y_{\text{12i4}}\forall \text{i}\in B]={\bar{y}}_{\text{124}}$$

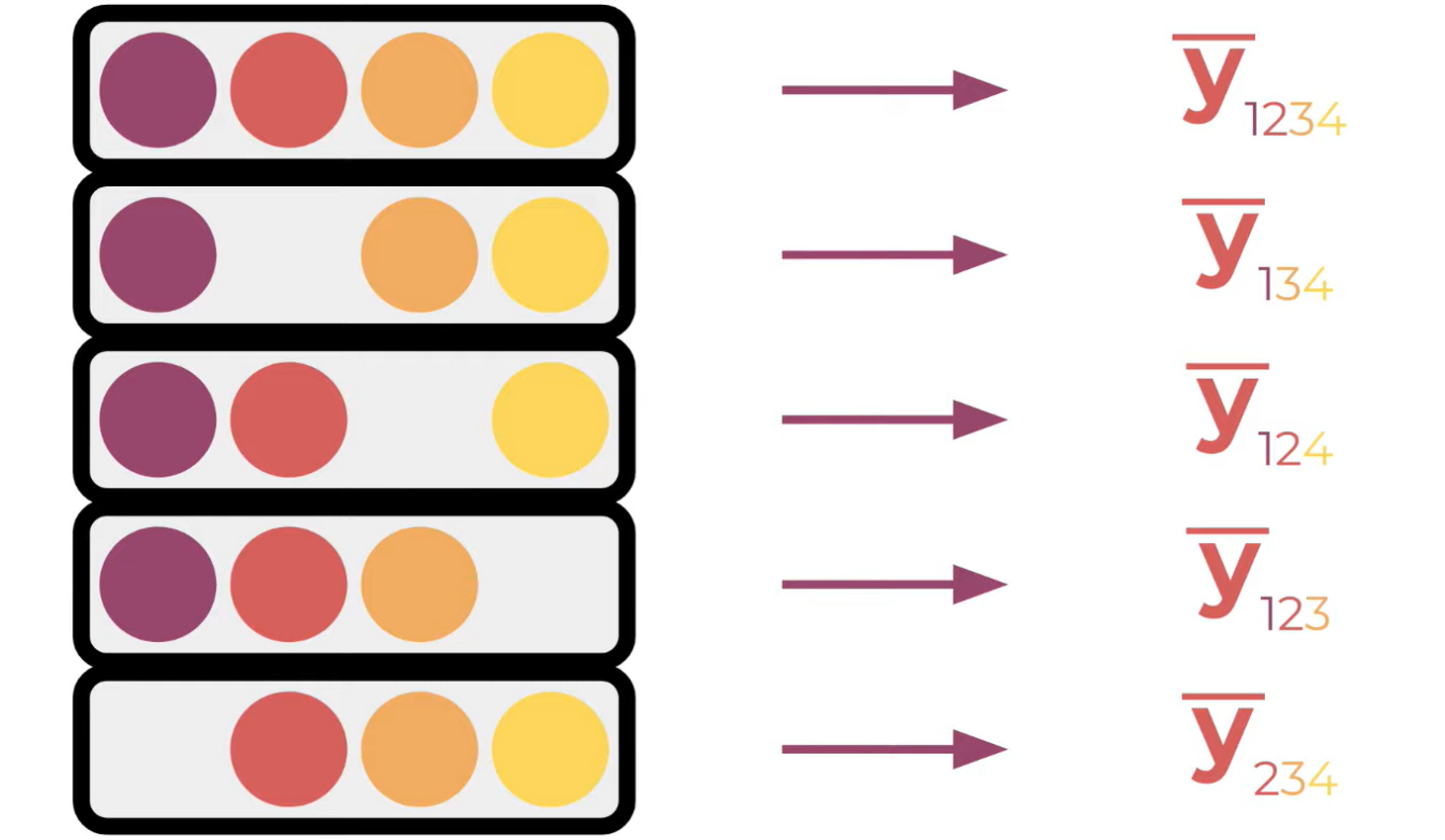
Them we have a number of samples computed in this way,like image in left.

We can formulate this as a weighted linear regression, with each feature assigned a coefficient.

And we can prove that, in the special choice, the coefficient can be the shaplely values. This weighting scheme is the basis of the Shapley Kernal. In this situation, the weighted linear regression process as a whole is Kernal SHAP.

Different types of SHAP

• Kernal SHAP
• Low-order SHAP
• Linear SHAP
• Max SHAP
• Deep SHAP
• Tree SHAP

You need to notice

We can see that, we calculate shapley values using linear regression lastly. So there must be the error here, but some python packages can not give us the error bound, so it’s confusion to konw if this error come from linear regression or the data, or the model.

Reference

Shapley Additive Explanations (SHAP)

SHAP: A reliable way to analyze your model interpretability

【Python可解释机器学习库SHAP】：Python的可解释机器学习库SHAP

Shapley Values : Data Science Concepts

Appendix

Other methods to interprete model:

Papers with Code - SHAP Explained