LLM hyperparameter

Temperature, Top-K, Top-P

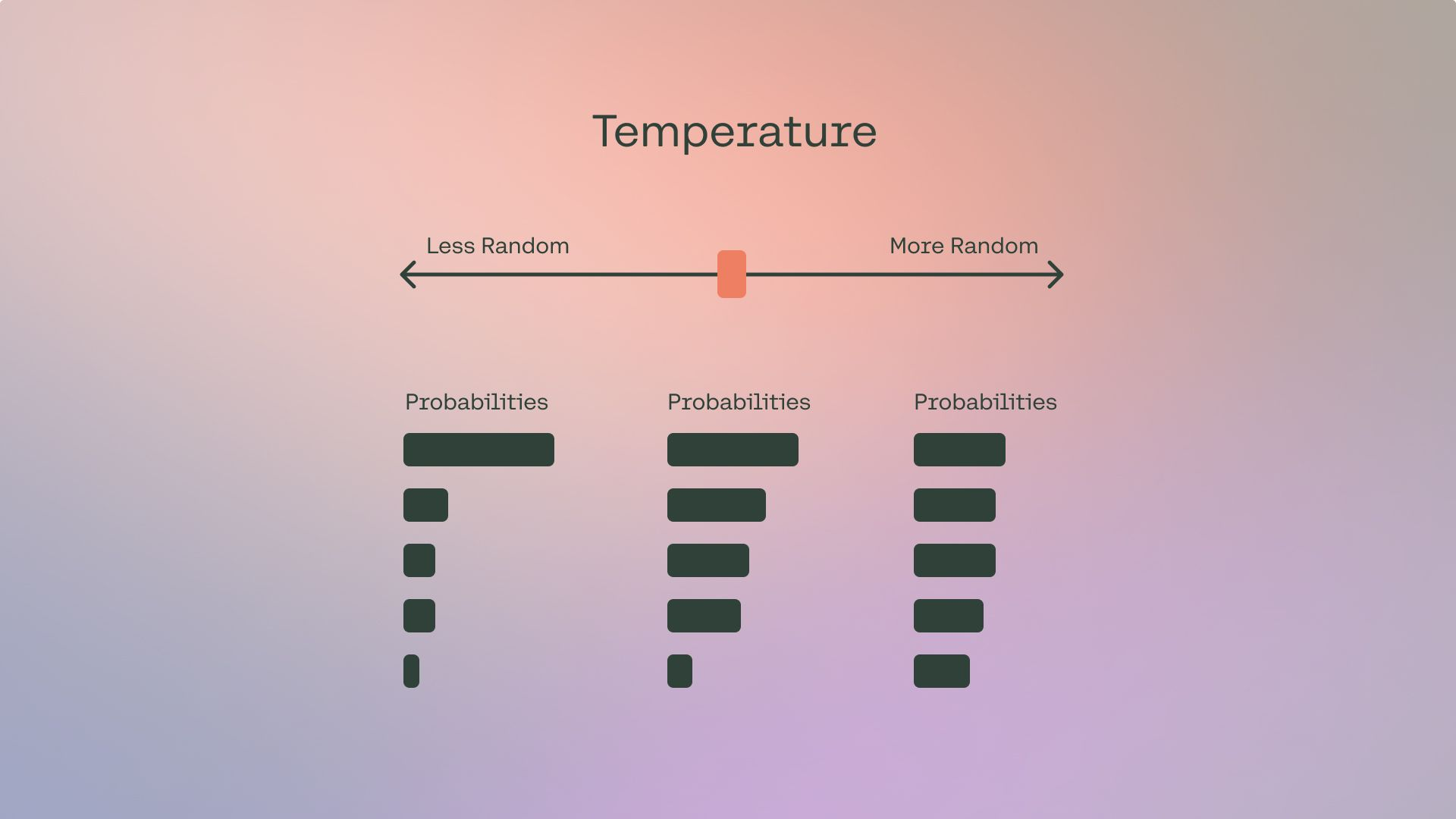
Temperature

Temperature definition come from the physical meaning of temperature. The more higher temperature, the atoms moving more faster, meaning more randomness.

LLM temperature is a hyperparameter that regulates the randomness, or creativity.

• Higher the LLM temperature, more diverse and creative, increasing likelihood of straying from context.
• Lower the LLM temperature, more focused and deterministic, sticking closely to the most likely prediction

More detail

The LLM model is to give a probability of next word, like this:

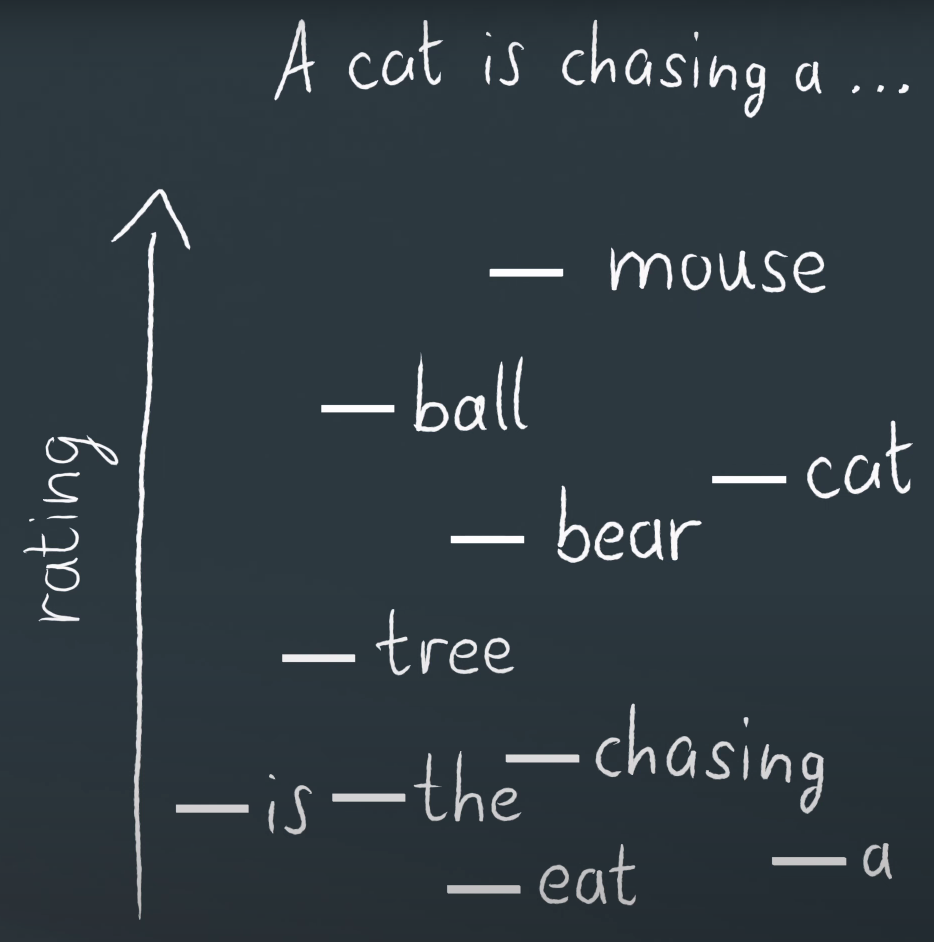
“A cat is chasing a …”, there are lots of words can be filled in that blank. Different words have different probabilities, in the model, we output the next word ratings.

Sure, we can always pick the highest rating word, but that would result in very standard predictable boring sentences, and the model wouldn’t be equivalent to human language, because we don’t always use the most common word either.

So, we want to design a mechanism that allows all words with a decent rating to occur with a reasonable probability, that’s why we need temperature in LLM model.

Like real physic world, we can do samples to describe the distribution, we use SoftMax to describe the distribution of the probability of the next word. The temperature is the element $T$ in the formula:

$$p_i=\frac{\exp (\frac{R_i}{T})}{{\sum }_i\exp (\frac{R_i}{T})}$$

More lower the $T$, the higher rating word’s probability will goes to 100%, and more higher the $T$, the probability will be more smoother for very words.

The gif below is important and intuitive.

So, set different $T$, the next word’s probability will be changed, we will output next word depending on the probability.

Top-K

Top-k limits the model’s output to the top-k most probable tokens at each step. This can help reduce incoherent or nonsensical output by restricting the model’s vocabulary.

With top-k sampling and let’s say K=5, it does the following:

• It considers only the top 5 highest probability words in the distribution after sorting them.
• It re-normalizes the probabilities among just those 5 words to sum to 1.
• It samples the next word from this re-normalized distribution over the top 5 words.

Top-P

Top-p filters out tokens whose cumulative probability is less than a specified threshold (p). It allows for more diversity in the output while still avoiding low-probability tokens.

For example, let’s say after “I’ll have the…” the words and their probabilities are:

salad: 0.4  
burger: 0.3  
pasta: 0.1  
steak: 0.08

With Top-P=0.8, it will include salad (0.4), burger (0.3), pasta (0.1) since 0.4 + 0.3 + 0.1 = 0.8. This covers 80% of the probability mass in just the top 3 words.

So the model now samples from just {salad, burger, pasta} instead of the full vocabulary.

Min-P

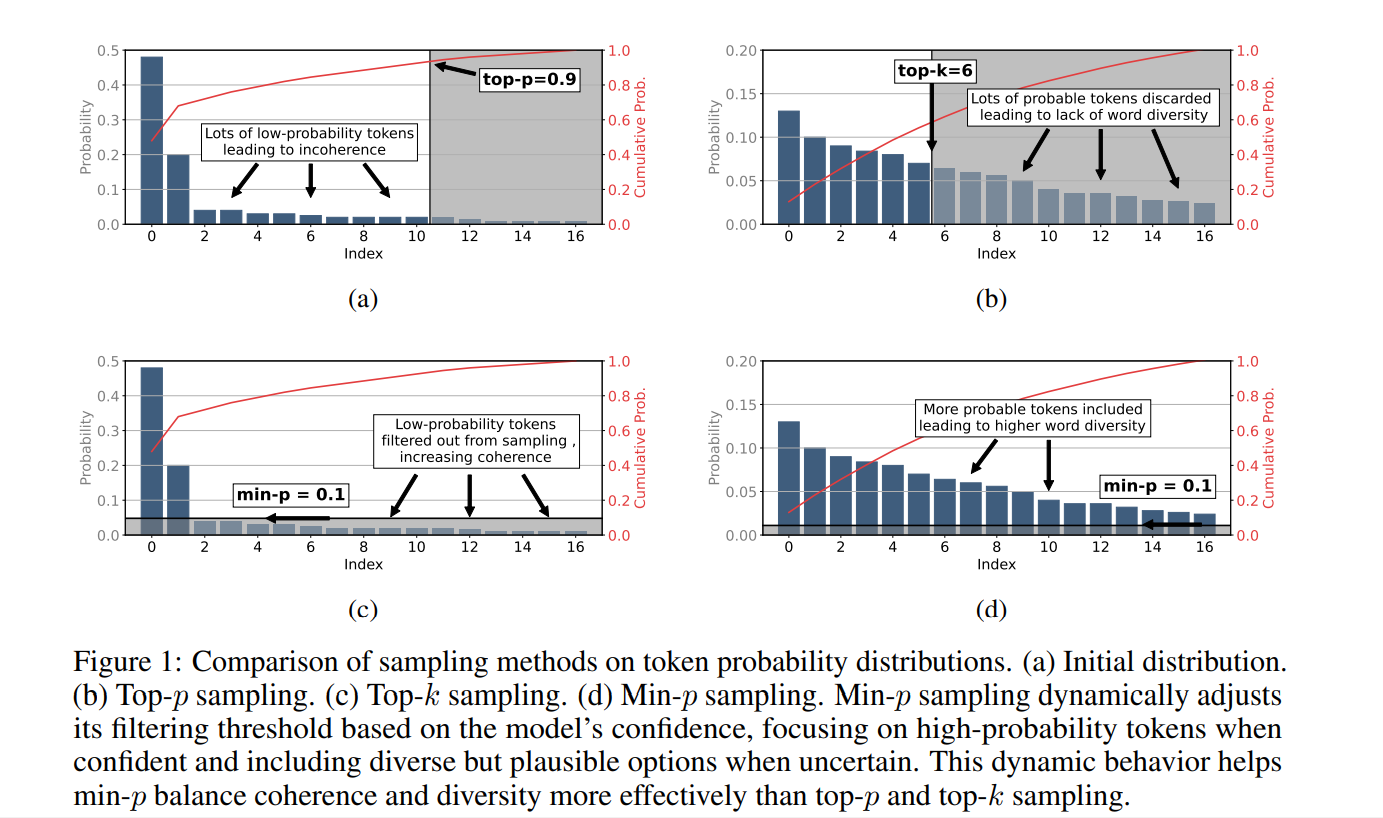
Min-P was proposed after Top-K and Top-P. The motivation is that somebody found the “flaws” in the popular Top-P sampling method:

• When the model does not have sufficient confidence/concentration on the next token candidate(s), it’s possible for the sampler to consider many tokens that are highly unlikely compared to the few choices it has confidence in.
• Top K helps limit the amount of ‘low confidence’ tokens period as a supplement to Top P, but this often comes at a cost of token choice diversity (often arbitrarily).
• In addition to this, Top P can sometimes cut reasonable tokens. What if there’s a 90.1% probability token, followed by a 9% probability token? A Top P value of 0.90 would completely gloss over the 9% token in this instance.

Interaction between Temperature, Top-K, Top-P, Min-P

Let’s start with an example by setting the parameters Temperature = 0.8, Top-K = 35, Top-P = 0.7, Min-P = 0.1

1. First, the model computes the full unnormalized log probability distribution over the entire vocabulary based on the previous context.
2. It applies the Temperature=0.8 scaling by dividing each log probability by 0.8.
3. It selects the 35 tokens with the highest scaled log probabilities
4. From this Top-K=35 set, it applies the Top-P=0.7 filtering. Keeping tokens in order until their cumulative probability mass reaches 0.7 or 70%
5. Min-P = 0.1, removes options with less than 10% probability of top option.
6. Finally,  renormalizes just the scaled log probabilities of these final tokens to sum to 1

Mirostat

Perplexity

Perplexity is defined as the exponentiated average negative log-likelihood of a sequence. If we have a tokenized sequence$X=(x_0,x_1,\dots ,x_t)$, then the perplexity of $X$ is,

$$PPL(X)=\exp \{-\frac{1}{t}\sum _i^t\log p_{\theta }(x_i|x_{<i})\}$$

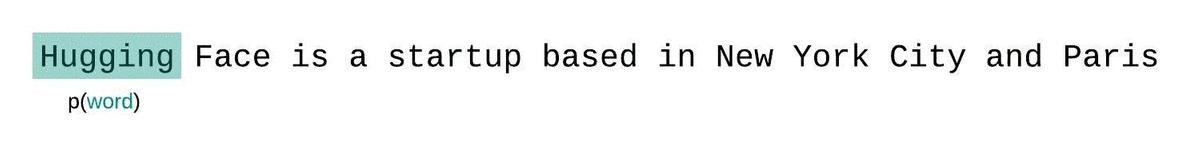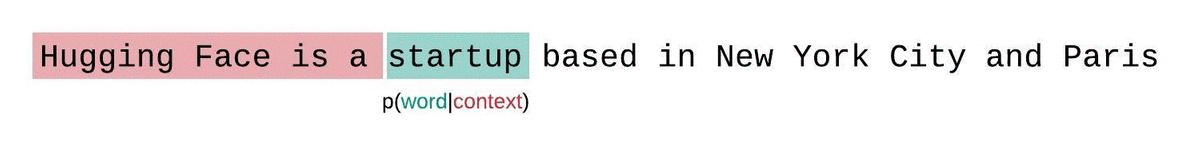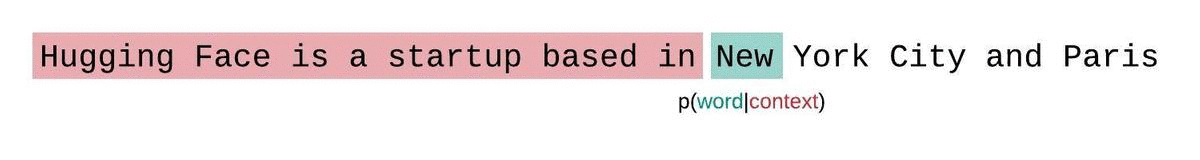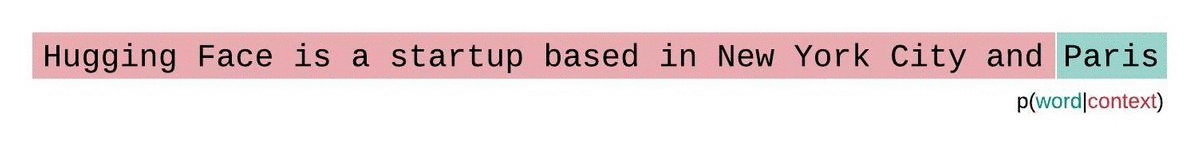
Reference

• LLM Temperature, dedpchecks
• ⭐⭐⭐https://www.youtube.com/watch?v=YjVuJjmgclU
• https://rumn.medium.com/setting-top-k-top-p-and-temperature-in-llms-3da3a8f74832
• https://github.com/huggingface/transformers/issues/27670
• https://ar5iv.labs.arxiv.org/html/2007.14966
• https://huggingface.co/docs/transformers/perplexity