Segment Tree

Overview

Segment Tree（线段树）是一种用于解决区间查询问题的数据结构。它可以有效地处理包含大量区间操作的问题，如查询区间最大值、最小值、求和、更新等。

Segment Tree将给定的区间划分为若干个较小的子区间，并使用树进行表示。每个节点表示一个子区间，树的根节点表示整个区间。每个节点记录了对应子区间的一些统计信息，如该区间的最大值、最小值、总和等。

构建Segment Tree的过程中，首先将问题规模不断缩小，将大的区间划分为两个较小的子区间，并依次递归构建每个子区间的节点。当区间缩小到长度为1时，即叶子节点，将问题的原始数据作为叶子节点的值。

Segment Tree的构建完成后，可以高效地进行查询和更新操作。查询操作通过递归遍历树的节点，在给定的区间范围内查找所需的统计信息。更新操作通过递归更新树的节点，更新目标区间内的值，并更新父节点的统计信息。

由于Segment Tree的每个节点代表的区间是互不重叠的，因此在进行统计信息的查询和更新时，可以利用区间的性质进行剪枝操作，从而提高效率。

Detail

Basic

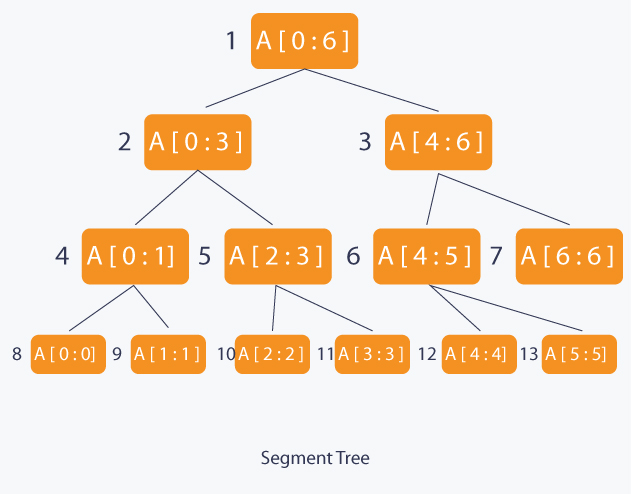
Segment Tree is a basically binary tree, we can represent segment tree in a simple linear array. We can learn segment tree by knowing some key points. We consider an array $A$ of size $N$ and a corresponding Segment Tree $T$.

1. The root of $T$ will represent the whole array $A[0:N-1]$
2.  In each step, the segment is divided into half and the two children represent those two halves. $A[0:N-1]$ will be divided into $A[0,(N-1)/2]$ & $A[(N-1)/2+1,N-1]$
3. Height of the segment tree will be $lo{g}_{2}N$. The internal nodes is $N-1$ and leaves are $N$. So a total number of nodes are $2\times N-1$.

Operations

Once the Segment Tree is built, its structure cannot be changed. We can update the values of nodes but we cannot change its structure. Segment tree provides two operations:

1. Update: To update the element of the array $A$ and reflect the corresponding change in the Segment tree.
2. Query: In this operation we can query on an interval or segment and return the answer to the problem (say minimum/maximum/summation in the particular segment).

Time Complexity and Code Implementation Demo

Build

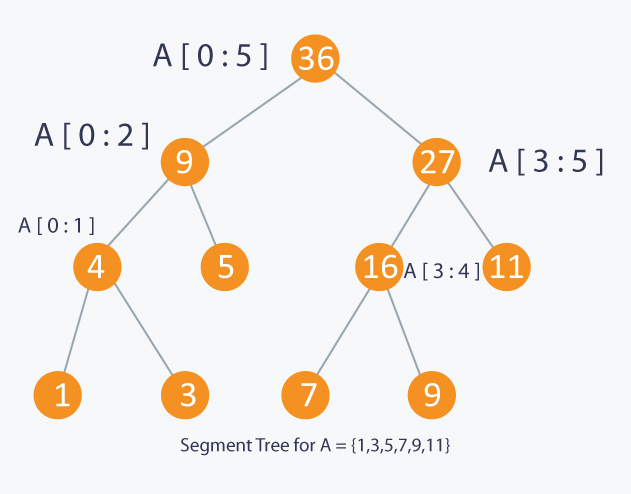
void build(int node, int start, int end)
{
    if(start == end)
    {
        // Leaf node will have a single element
        tree[node] = A[start];
    }
    else
    {
        int mid = (start + end) / 2;
        // Recurse on the left child
        build(2*node, start, mid);
        // Recurse on the right child
        build(2*node+1, mid+1, end);
        // Internal node will have the sum of both of its children
        tree[node] = tree[2*node] + tree[2*node+1];
    }
}

def segment_tree_build(nums):
    n = len(nums)
    tree = np.zeros(2 * n)
    
    tree[n:2 * n] = nums
    
    for i in range(n-1, 0, -1):
        tree[i] = tree[2 * i] + tree[2 * i + 1]
        
    return tree

Every nodes means a sum of an interval. Build Complexity is $O(N)$

Update

void update(int node, int start, int end, int idx, int val)
{
    if(start == end)
    {
        // Leaf node
        A[idx] += val;
        tree[node] += val;
    }
    else
    {
        int mid = (start + end) / 2;
        if(start <= idx and idx <= mid)
        {
            // If idx is in the left child, recurse on the left child
            update(2*node, start, mid, idx, val);
        }
        else
        {
            // if idx is in the right child, recurse on the right child
            update(2*node+1, mid+1, end, idx, val);
        }
        // Internal node will have the sum of both of its children
        tree[node] = tree[2*node] + tree[2*node+1];
    }
}

To update an element, look at the interval in which the element is present and recurse accordingly on the left or the right child.

Complexity of update will be $O(logN)$

Query

int query(int node, int start, int end, int l, int r)
{
    if(r < start or end < l)
    {
        // range represented by a node is completely outside the given range
        return 0;
    }
    if(l <= start and end <= r)
    {
        // range represented by a node is completely inside the given range
        return tree[node];
    }
    // range represented by a node is partially inside and partially outside the given range
    int mid = (start + end) / 2;
    int p1 = query(2*node, start, mid, l, r);
    int p2 = query(2*node+1, mid+1, end, l, r);
    return (p1 + p2);
}

将查询区间切割成多个区间在不同节点查找并合并

LazyTag Trick

Lazy Tag的设计目的是为了[l, r]区间所有数增加k的情况，做多次update时间复杂度浪费过多，利用lazy tag降低时间复杂度。

lazy tag的设计原理是，被打上lazy tag的seg node是已经更新完了的seg node，而lazy tag之下的seg node是没有更新的。只有要访问lazy tag之下的seg node的时候才去做更新，来节省更新。

Lazy Tag Propagation

lazy propagation is a optimize technique in segment tree to minimize tons of operations.

lazy propagation is hard to explain, so watch this tutorial vedio is a best way to learn and review.

pls watch vedio in reference 3: Lazy Propagation Segment Tree. www.youtube.com, https://www.youtube.com/watch?v=xuoQdt5pHj0. Accessed 12 Sept. 2023.

Reference

• “Segment Trees Tutorials & Notes | Data Structures.” HackerEarth, https://www.hackerearth.com/practice/data-structures/advanced-data-structures/segment-trees/tutorial/. Accessed 7 Sept. 2023.
• “力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台.” 力扣 LeetCode, https://leetcode.cn/problems/handling-sum-queries-after-update/solutions/2356392/geng-xin-shu-zu-hou-chu-li-qiu-he-cha-xu-kv6u/. Accessed 11 Sept. 2023.
• Lazy Propagation Segment Tree. www.youtube.com, https://www.youtube.com/watch?v=xuoQdt5pHj0. Accessed 12 Sept. 2023.