Topological Sorting

What is Topological Sorting

Topological Sorting(拓扑排序) is designed for Directed Acyclic Graph(DAG, 有向无环图). Topological Sorting is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering.

Example

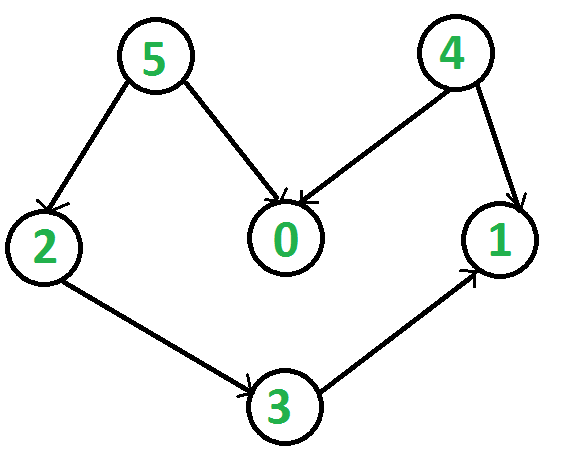
Topological sorting can be more than one result. For this graph, “5 4 2 3 1 0” is one of the result. The first vertex in topological sorting is always a vertex with an in-degree of 0.

Algorithm to do Topological Sorting

DFS

深度优先搜索以任意顺序循环遍历图中的每个节点，若搜索进行中碰到之前已经遇到的节点，或碰到叶节点，则中止算法。

L ← Empty list that will contain the sorted nodes
while exists nodes without a permanent mark do
	select an unmarked node n
	visit(n)
 
function visit(node n)
	if n has a permanent mark then
		return
	if n has a temporary mark then
		return error (graph not DAG)
 
	mark n with a temporary mark
	
	for each node  m with a edge from n to m do
		visit(m)
	
	remove temporary mark from n
	mark n with a permanent mark
	add n to head of L

Kahn’s Algorithm

 First, find a list of “start nodes” which have no incoming edges and insert them into a set S; at least one such node must exist in a non-empty acyclic graph

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge
 
while S is not empty do
 
	remove a node n from S
	add n to L
	
	for each node m with an edge e from n to m do
		remove edge e from graph
		
		if m has no other incoming edge then
			insert m into S
	
	if graph has edges then
		return error (graph no DAG)
	else
		return L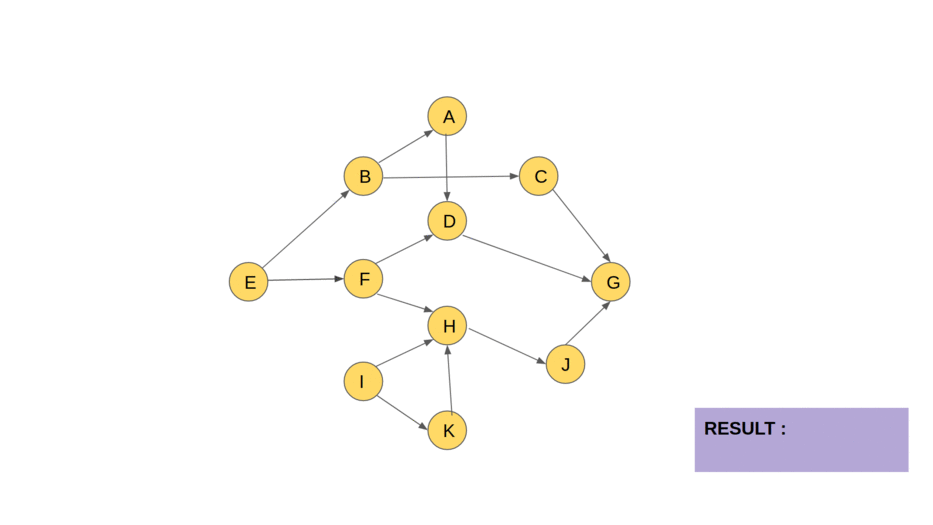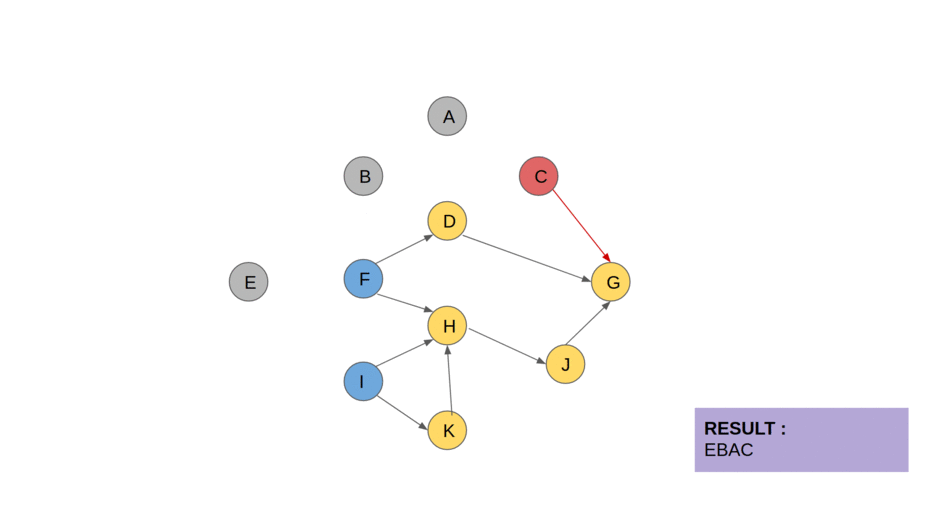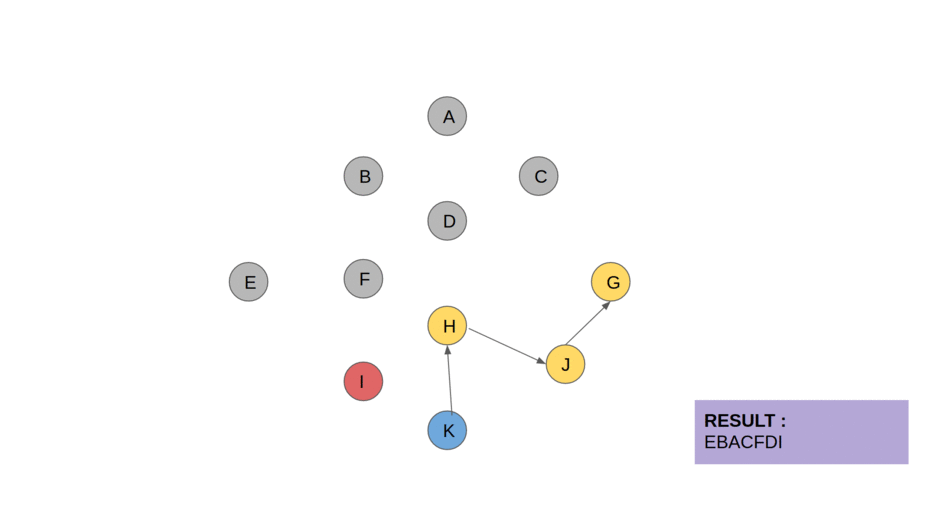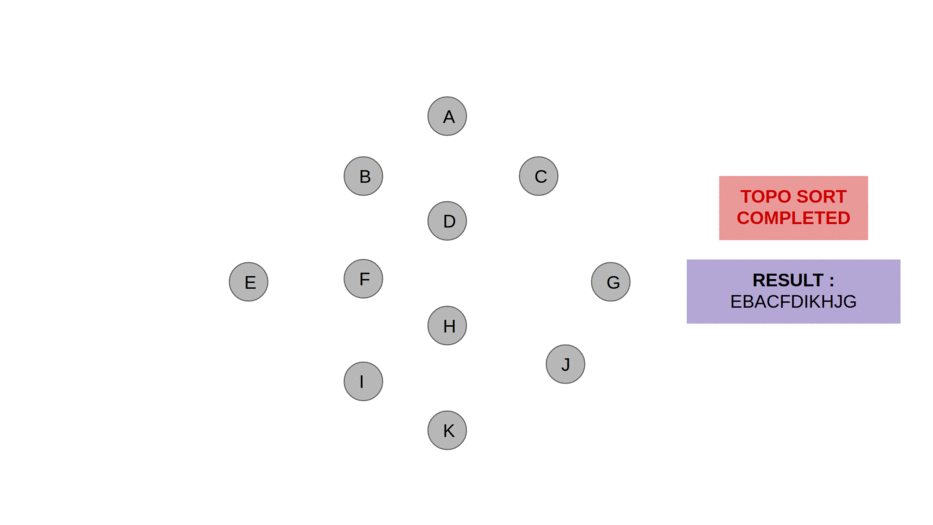

Topological Sorting Application

• Task Priorities

Reference

• “Topological Sorting.” GeeksforGeeks, 12 May 2013, https://www.geeksforgeeks.org/topological-sorting/.
• “拓撲排序.” 维基百科，自由的百科全书, 22 May 2022. Wikipedia, https://zh.wikipedia.org/w/index.php?title=%E6%8B%93%E6%92%B2%E6%8E%92%E5%BA%8F&oldid=71758255.
• “算法 - 拓扑排序.” Earth Guardian, 22 Aug. 2018, http://redspider110.github.io/2018/08/22/0092-algorithms-topological-sorting/index.html.